Dimensionless quantities for the light field, and introduction of a coupling constant

In the following we shall introduce dimensionless variables b_λ and b_λ^* instead of the mode amplitudes E_λ⁽⁺⁾ and E_λ^(-) respectively. The quantities E_λ and b_λ differ by a simple factor only, namely

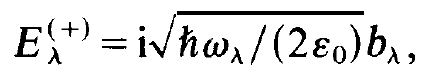  (1.1)

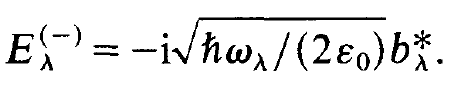    (1.2)

As one may show, the energy of an electric field with mode amplitude E_λ is proportional to |E_λ|². On the other hand, in a quantum theoretical treatment h⍵_λ is just the energy of a photon. Since b_λ is dimensionless we recognize that |b_λ|² must have the meaning of a photon number, may be except for a numerical factor. As it will turn out later, |b_λ|² is precisely the average photon number. We shall elucidate this relation in a later chapter when dealing with the laser equations quantum theoretically. We then recognize that there always the combination ϑ₂₁ u_λ (x_μ)occur s (or the conjugate complex quantity). Furthermore the factor  occurs. In order to save space it suggests itself to replace this combination by a quantity which we define by

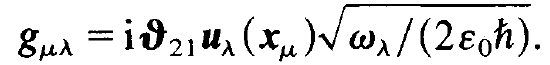   (1.3)

It is a rather simple but boring task to rewrite the laser equations by means of the new quantities just introduced. Therefore we shall write down the laser equations in the next section without any intermediate steps

مواضيع ذات صلة

الليزرات والسوائل التي تصعد إلى الأعلى

الليزر والميزر

Flashtube Explosion

Tube Failure

Plane–Parallel Resonator

Concave–Convex Resonator

Plano-Concave Resonator

Mirrors of Equal Curvature

Parasitic Oscillations

Prelasing

Depopulation Losses

The Three-Level System