The semiclassical laser equations for the macroscopic quantities electric field strength, polarization, and inversion density

By simple transformations, equations for the macroscopic polarization and the inversion density may be derived from

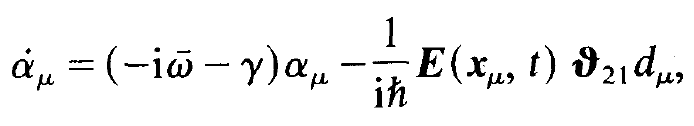   (i)

and

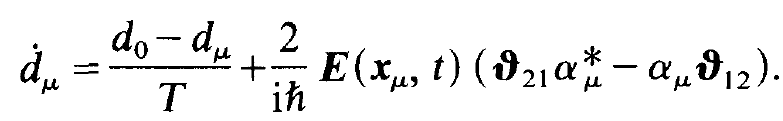    (ii)

Because we shall not immediately make use of these equations in the subsequent sections, the speedy reader can skip this section. Once again we consider. When we insert the further in it, it suggests itself to introduce the new quantity

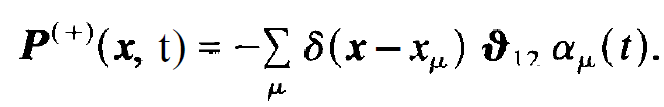    (1.1)

We denote the quantity conjugate complex to P⁽⁺⁾ by P^(-)

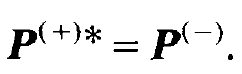    (1.2)

In a way analogous to (1.1) we define the inversion density by summing up over the individual atoms using Dirac's 8-function

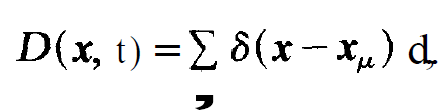    (1.3)

It will be our goal to derive from eqs. (i) and (ii) equations for the macroscopic quantities P and D. To this end we multiply (i) on both sides by 6 (x - x_μ)ϑ­₁₂ and sum up over μ. The term 6(x - x_μ) E(x_μ, t) occurring in it may be replaced by

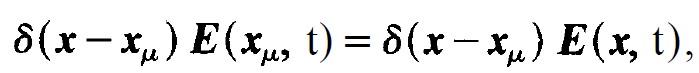 (1.4)

(compare exercise). Thus we immediately obtain the relation

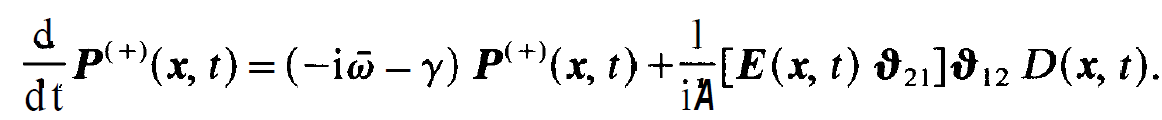 (1.5)

We proceed in a similar way with eq. (ii) and obtain

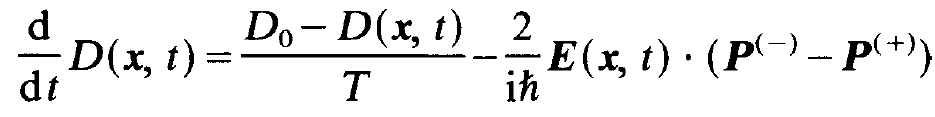    (1.6)

where we have introduced the total inversion D₀, which is produced by the incoherent processes, according to the relation

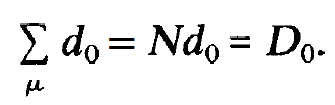 (1.7)

مواضيع ذات صلة

الليزرات والسوائل التي تصعد إلى الأعلى

الليزر والميزر

Flashtube Explosion

Tube Failure

Plane–Parallel Resonator

Concave–Convex Resonator

Plano-Concave Resonator

Mirrors of Equal Curvature

Parasitic Oscillations

Prelasing

Depopulation Losses

The Three-Level System