Quantitative treatment of hole burning. Single mode laser action of an inhomogeneously broadened line

We now return to single mode laser action in a solid state laser with an inhomogeneously broadened line. We start from the mode which we write down for the special case of a single mode where we drop the index A of n but retain it for sake of clarity in W_λμ. Neglecting as usual spontaneous emission this equation reads

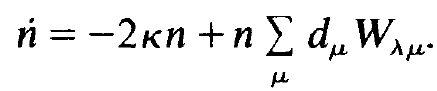   (1.1)

We insert in it the saturated inversion reads

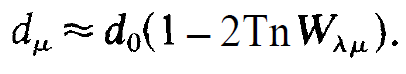     (1.2)

We adopt running waves so that W_λμ does no more depend on the space coordinate x. Using the explicit form of W_λμ as and replacing the index μ by I we may write

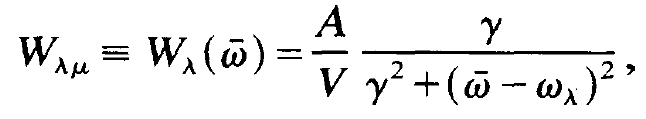    (1.3)

where we have used the abbreviation

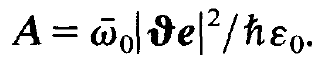    (1.4)

By inserting (1.2) into (1.1) we cast eq. (1.1) into the form

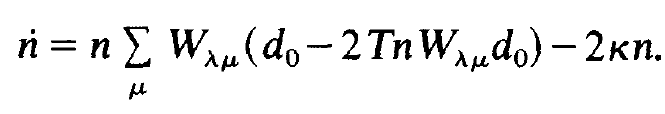    (1.5)

We convert the sum over the atomic indices μ into an integral over space and an integral over the frequencies ,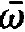

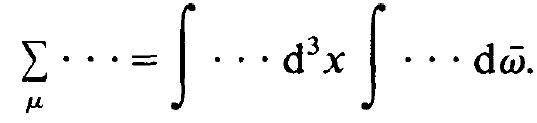    (1.6)

Because W does not depend on space the integration over the volume elements d³x yields the volume V of the resonator. In order to evaluate the integral over I we use a Gaussian distribution for the frequency distribution

ρ(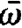), i.e.

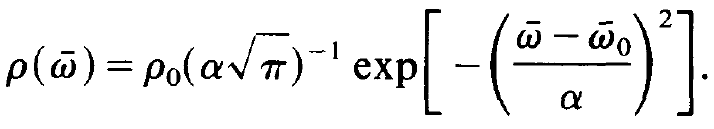     (1.7)

Here ρ₀ is the density of atoms, ρ₀ = N/ V, where N is the total number of laser atoms in the resonator and V the volume of the resonator, and a is the half width of the Gaussian distribution. We first treat the first term on the r.h.s. of (1.5),

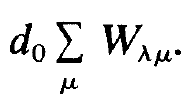    (1.8)

In order to evaluate this expression we insert (1.3) and (1.7) into it. Observing that integration over the volume in (1.6) cancels against V in the denominator in (1.3) we have eventually to treat

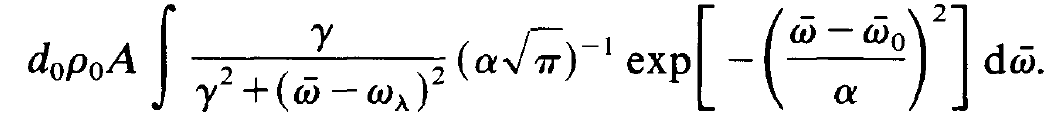    (1.9)

This integral cannot be evaluated in explicit form. However, it is rather simple to calculate it approximately if we assume y << a. In such a case we obtain in a good approximation

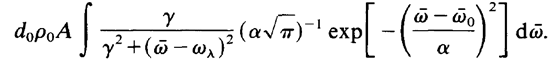
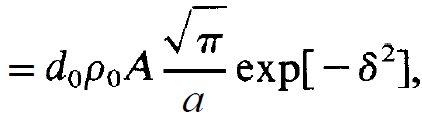 (1.10)

where δ is defined by

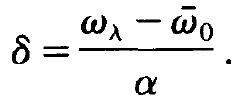    (1.11)

In a similar fashion we can evaluate the second term in (1.5), i.e.

    (1.12)

which yields

    (1.13)

Taking the corresponding terms together, we may cast (1.5) into the explicit form

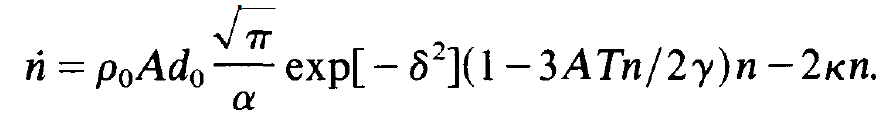     (1.14)

the stationary state, dn/dt = 0, this equation can be readily solved for n. Because n is the only free parameter in the formula for hole burning, (1.2), we have thus fixed the depth of that hole. We mention that the integrals such as (1.9) can be evaluated exactly and explicitly if the inhomogeneous atomic line is a Lorentzian.

مواضيع ذات صلة

الليزرات والسوائل التي تصعد إلى الأعلى

الليزر والميزر

Flashtube Explosion

Tube Failure

Plane–Parallel Resonator

Concave–Convex Resonator

Plano-Concave Resonator

Mirrors of Equal Curvature

Parasitic Oscillations

Prelasing

Depopulation Losses

The Three-Level System