الحركة في منحني

في هذا النوع من الحركة تكون سرعة الجسم عند أي نقطة على المسار باتجاه مماس المسار عند تلك النقطة . وبما ان اتجاه السرعة يتغير من نقطة إلى اخرى على المسار ، فإن سرعة الجسم تكون متغيرة حتى ولو كانت ثابتة في المقدار.

‏يبن الشكل (1) دقيقة مادية تتحرك على مسار منحن سرعتها عند A هي V₁ وسرعتها عند النقطة B  هي V₂ . وعند إيجاد (V) ، فإننا نزيح المتجه V₂ موازيا لنفسه بحيث تنطبق نقطة بدايته V₁ على نقطة بداية (V) ، ثم نكمل المثلث لإيجاد (V‏) . وحيث ان الزمن الذي احتاجته الدقيقة في الحركة من (A‏) إلى (B‏) هو (t)، فإن متوسط تسارع الدقيقة في المسار المنحني هو ((a_av حيث :

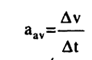................(1)

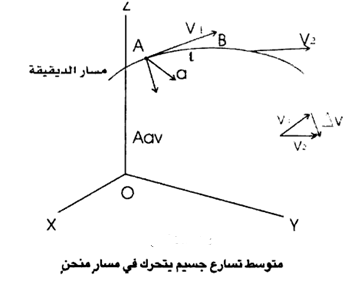
الشكل (1)

وهذا التسارع  دائما يشير إلى مركز المسار المنحني ؛ ولذلك يطلق عليه اسم التسارع المركزي Centripetal" " أي باتجاه المركز، ويرمز له بالرمز (a_N) .

‏ولو افترضنا أن النقطة (B) أصبحت قريبة جدا من (A) بحيث تؤول t)) إلى الصفر، فان (v) تكون باتجاه السرعة (v₁) عند النقطة (A) ؛ وعليه سيكون التسارع باتجاه السرعة (v₁) ، أي ان التسارع يكون مماسا للمسار عند السرعة اللحظية ؛ لذلك ، يسمى هذا التسارع بالتسارع المماسي (ar) . إذن متوسط التسارع الكلي للجسم الذي يسير في منحنى هو :

                              (2) …………         a=a_N+a_r

‏وعليه ، فإن التسارع الكلي للجسيم الذي يسير في منحنى (a‏)، لا يكون مماسا للمسار ولا عموميا على المماس للمسار ، بل باتجاه محصلة التسارعين (a_T , a_N) ‏وعليه نستطيع ان نثبت الحقيقتين التاليتين :

1- التغير في مقدار السرعة يؤيد إلى التسارع المماسي .

2- التغير في اتجاه السرعة يؤدي إلى التسارع المركزي aN .

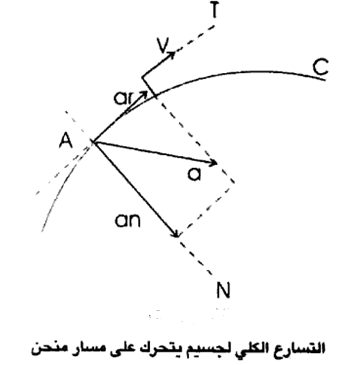
الشكل (2)

ويمكن إثبات أن كلا من التسارع المركزي والتسارع المماسي يعطيان بالمعادلتين التاليتين :

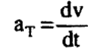............(أ3)

.(ب3)............

حيث (v) هي السرعة الثابتة للجسم على المنحنى ، (R) هي نصف قطر المسار المنحنى فإذا كانت السرعة ثابتة من حيث المقدار ، فإن :

أي انه لا يوجد تسارع مماسي ، في حين انه اذا كانت الحركة خطية (أي في خط مستقيم) فإن   R  أي أن a_N=0 وبالتالي لا يوجد تسارع مركزي .

مواضيع ذات صلة

أنظمة لأكثر من جسيم واحد

كمية التحرك الزاوية والقوة المركزية

الحركة الدورانية

امثلة عن الاتزان الاستاتيكي للأجسام الممتدة

الاتزان الاستاتيكي للأجسام الممتدة

تعريف العزم

تذبذبات صغيرة لبندول

اعتبارات الطاقة في الحركة التوافقية البسيطة

الحل الهندسي للمعادلة التفاضلية للحركة التوافقية البسيطة، دائرة المرجع

الحل باستخدام حساب التفاضل والتكامل

قانون هوك والمعادلة التفاضلية للحركة التوافقية البسيطة

القدرة ووحدات الشغل