The smallest value of a set, function, etc. The minimum value of a set of elements {a_i}_(i=1)^N" src="http://mathworld.wolfram.com/images/equations/Minimum/Inline1.gif" style="height:19px; width:64px" /> is denoted 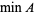 or 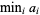, and is equal to the first element of a sorted (i.e., ordered) version of 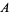. For example, given the set {3,5,4,1}" src="http://mathworld.wolfram.com/images/equations/Minimum/Inline5.gif" style="height:14px; width:62px" />, the sorted version is {1,3,4,5}" src="http://mathworld.wolfram.com/images/equations/Minimum/Inline6.gif" style="height:14px; width:62px" />, so the minimum is 1. The maximum and minimum are the simplest order statistics.

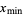The minimum value of a variable  is commonly denoted  (cf. Strang 1988, pp. 286-287 and 301-303) or  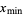(Golub and Van Loan 1996, p. 84). In this work, the convention  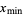is used.

The minimum of a set of elements is implemented in the Wolfram Language as Min[list] and satisfies the identities

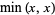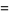			(1)
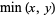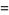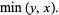			(2)

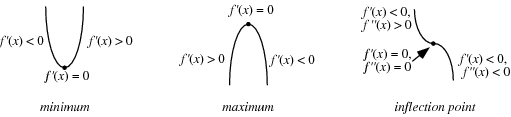
A continuous function may assume a minimum at a single point or may have minima at a number of points. A global minimum of a function is the smallest value in the entire range of the function, while a local minimum is the smallest value in some local neighborhood.

For a function 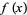 which is continuous at a point 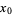, a necessary but not sufficient condition for  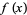to have a local minimum at  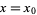is that  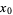be a critical point (i.e.,  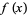is either not differentiable at  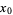or 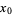 is a stationary point, in which case ).

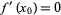The first derivative test can be applied to continuous functions to distinguish minima from maxima. For twice differentiable functions of one variable, 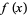, or of two variables, 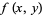, the second derivative test can sometimes also identify the nature of an extremum. For a function 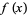, the extremum test succeeds under more general conditions than the second derivative test.

Definite integral include

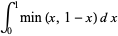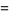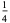			(3)
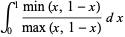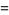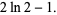			(4)

REFERENCES:

Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 14, 1972.

Brent, R. P. Algorithms for Minimization Without Derivatives. Englewood Cliffs, NJ: Prentice-Hall, 1973.

Golub, G. and Van Loan, C. Matrix Computations, 3rd ed. Baltimore, MD: Johns Hopkins University Press, 1996.

Nash, J. C. "Descent to a Minimum I-II: Variable Metric Algorithms." Chs. 15-16 in Compact Numerical Methods for Computers: Linear Algebra and Function Minimisation, 2nd ed. Bristol, England: Adam Hilger, pp. 186-206, 1990.

Niven, I. Maxima and Minima without Calculus. Washington, DC: Math. Assoc. Amer., 1982.

Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. "Minimization or Maximization of Functions." Ch. 10 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 387-448, 1992.

Strang, G. Linear Algebra and its Applications, 3rd ed. Philadelphia, PA: Saunders, 1988.

Tikhomirov, V. M. Stories About Maxima and Minima. Providence, RI: Amer. Math. Soc., 1991.

اخر الاخبار

اخبار العتبة العباسية المقدسة

قسم التطوير يقيم دورة عن أخلاقيات المهنة للمنتسبين الجدد

تتضمن زيارة المراقد المقدسة في كربلاء.. معهد القرآن الكريم النسوي ينظم سفرة دينية لطالباته

المجمع العلمي يحتفي بذكرى ولادة الإمامين الباقر والهادي (عليهما السلام)

قسم الشؤون الفكرية يطلق فعاليات الأسبوع الثالث من برنامج البذرة الصالحة

المزيد

الآخبار الصحية

ثورة طبية.. الذكاء الاصطناعي يكشف سرطان الكلى في وقت قياسي

لتعزيز الطاقة والتغلب على التعب.. عليك بـ7 طرق بسيطة

لتحسين الهضم والتحكم في الشهية.. ما أفضل وقت لتناول التمر؟

خبراء يكشفون تأثير الاستحمام في الظلام على جودة النوم !

المزيد

الآخبار التكنلوجية

إزالة ثاني أكسيد الكربون من الغلاف الجوي.. ما دور المحيطات والبحار؟

نظائر الهيليوم مقياس لاكتشاف رواسب الذهب.. كيف ذلك؟

الصين تطلق أول ناقلة نفط خام ذكية في العالم تعمل بالميثانول

الزمن على المريخ أسرع من الأرض.. دراسة علمية تكشف الفوارق

المزيد