

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Unit Square Integral
المؤلف:
Bailey, D. H.; Borwein, J. M.; Calkin, N. J.; Girgensohn, R.; Luke, D. R.; and Moll, V. H
المصدر:
Experimental Mathematics in Action. Wellesley, MA: A K Peters, 2007.
الجزء والصفحة:
...
17-9-2018
4694
Unit Square Integral
Integrals over the unit square arising in geometric probability are
![int_0^1int_0^1sqrt(x^2+y^2)dxdy=1/3[sqrt(2)+sinh^(-1)(1)]
int_0^1int_0^1sqrt((x-1/2)^2+(y-1/2)^2)dxdy
=1/6[sqrt(2)+sinh^(-1)(1)],](http://mathworld.wolfram.com/images/equations/UnitSquareIntegral/NumberedEquation1.gif) |
(1) |
which give the average distances in square point picking from a point picked at random in a unit square to a corner and to the center, respectively.
Unit square integrals involving the absolute value are given by
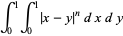 |
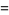 |
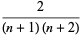 |
(2) |
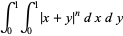 |
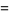 |
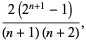 |
(3) |
for ![R[n]>-1](http://mathworld.wolfram.com/images/equations/UnitSquareIntegral/Inline7.gif) and
and ![R[n]>-2](http://mathworld.wolfram.com/images/equations/UnitSquareIntegral/Inline8.gif) , respectively.
, respectively.
Another simple integral is given by
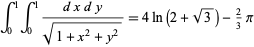 |
(4) |
(Bailey et al. 2007, p. 67). Squaring the denominator gives
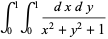 |
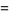 |
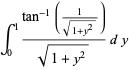 |
(5) |
 |
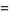 |
![int_0^11/(sqrt(4x^2-1))[tan^(-1)(3/(sqrt(4x^2-1)))-tan^(-1)((1+2x^2)/(sqrt(4x^2-1)))]dx](http://mathworld.wolfram.com/images/equations/UnitSquareIntegral/Inline14.gif) |
(6) |
 |
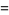 |
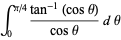 |
(7) |
 |
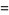 |
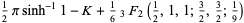 |
(8) |
 |
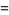 |
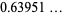 |
(9) |
(OEIS A093754; M. Trott, pers. comm.), where 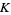 is Catalan's constant and
is Catalan's constant and 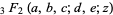 is a generalized hypergeometric function. A related integral is given by
is a generalized hypergeometric function. A related integral is given by
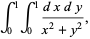 |
(10) |
which diverges in the Riemannian sense, as can quickly seen by transforming to polar coordinates. However, taking instead Hadamard integral to discard the divergent portion inside the unit circle gives
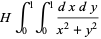 |
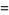 |
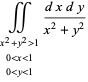 |
(11) |
 |
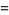 |
![int_0^11/x[tan^(-1)(1/x)-tan^(-1)((sqrt(1-x^2))/x)]dx](http://mathworld.wolfram.com/images/equations/UnitSquareIntegral/Inline31.gif) |
(12) |
 |
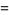 |
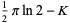 |
(13) |
 |
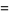 |
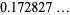 |
(14) |
(OEIS A093753), where 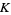 is Catalan's constant.
is Catalan's constant.
A collection of beautiful integrals over the unit square are given by Guillera and Sondow (2005) that follow from the general integrals
![int_0^1int_0^1(x^(u-1)y^(v-1))/(1-xyz)[-ln(xy)]^sdxdy](http://mathworld.wolfram.com/images/equations/UnitSquareIntegral/Inline39.gif) |
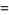 |
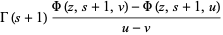 |
(15) |
![int_0^1int_0^1((xy)^(u-1))/(1-xyz)[-ln(xy)]^sdxdy](http://mathworld.wolfram.com/images/equations/UnitSquareIntegral/Inline42.gif) |
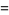 |
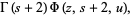 |
(16) |
for 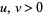 ,
, ![R[s]>-2](http://mathworld.wolfram.com/images/equations/UnitSquareIntegral/Inline46.gif) if
if 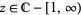 , and
, and ![R[s]>-1](http://mathworld.wolfram.com/images/equations/UnitSquareIntegral/Inline48.gif) if
if 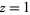 , where
, where 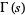 is the gamma function and
is the gamma function and 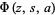 is the Lerch transcendent. In (15), to handle the case
is the Lerch transcendent. In (15), to handle the case 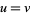 , take the limit as
, take the limit as 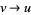 , which gives (16).
, which gives (16).
Another result is
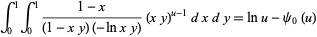 |
(17) |
(Guillera and Sondow 2005), for 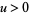 and where
and where 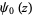 is the digamma function.
is the digamma function.
Guillera and Sondow (2005) also give
![int_0^1int_0^1([-ln(xy)]^s)/(1-xy)dxdy](http://mathworld.wolfram.com/images/equations/UnitSquareIntegral/Inline56.gif) |
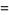 |
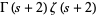 |
(18) |
![int_0^1int_0^1([-ln(xy)]^s)/(1+xy)dxdy](http://mathworld.wolfram.com/images/equations/UnitSquareIntegral/Inline59.gif) |
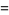 |
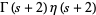 |
(19) |
![int_0^1int_0^1([-ln(xy)]^s)/(1+x^2y^2)dxdy](http://mathworld.wolfram.com/images/equations/UnitSquareIntegral/Inline62.gif) |
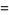 |
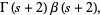 |
(20) |
where the first holds for ![R[s]>-1](http://mathworld.wolfram.com/images/equations/UnitSquareIntegral/Inline65.gif) , the second and third for
, the second and third for ![R[s]>-2](http://mathworld.wolfram.com/images/equations/UnitSquareIntegral/Inline66.gif) ,
, 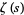 is the Riemann zeta function,
is the Riemann zeta function, 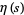 is the Dirichlet eta function, and
is the Dirichlet eta function, and 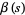 is the Dirichlet beta function. (19) was found by Hadjicostas (2002) for
is the Dirichlet beta function. (19) was found by Hadjicostas (2002) for 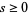 an integer. Formulas (18) and (19) are special cases of (16) obtained by setting
an integer. Formulas (18) and (19) are special cases of (16) obtained by setting 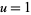 then taking
then taking 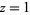 and
and 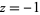 , respectively.
, respectively.
The beautiful formulas
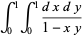 |
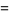 |
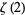 |
(21) |
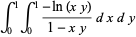 |
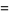 |
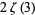 |
(22) |
were given by Beukers (1979). These integrals are special cases of (19) obtained by taking 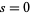 and 1, respectively. An analog involving Catalan's constant
and 1, respectively. An analog involving Catalan's constant 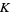 is given by
is given by
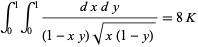 |
(23) |
(Zudilin 2003).
Other beautiful integrals related to Hadjicostas's formula are given by
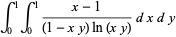 |
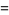 |
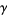 |
(24) |
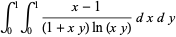 |
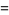 |
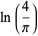 |
(25) |
(Sondow 2003, 2005; Borwein et al. 2004, p. 49), where 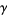 is the Euler-Mascheroni constant.
is the Euler-Mascheroni constant.
A collection of other special cases (Guillera and Sondow 2005) includes
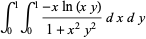 |
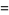 |
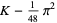 |
(26) |
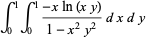 |
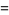 |
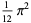 |
(27) |
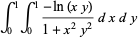 |
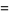 |
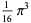 |
(28) |
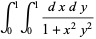 |
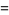 |
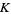 |
(29) |
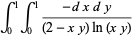 |
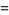 |
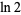 |
(30) |
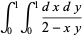 |
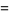 |
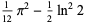 |
(31) |
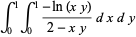 |
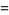 |
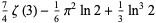 |
(32) |
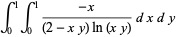 |
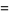 |
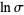 |
(33) |
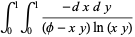 |
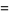 |
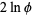 |
(34) |
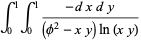 |
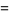 |
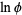 |
(35) |
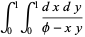 |
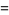 |
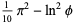 |
(36) |
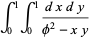 |
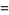 |
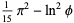 |
(37) |
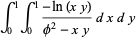 |
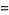 |
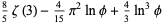 |
(38) |
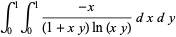 |
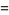 |
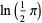 |
(39) |
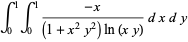 |
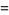 |
![ln[(sqrt(2pi))/(Gamma^2(3/4))]](http://mathworld.wolfram.com/images/equations/UnitSquareIntegral/Inline133.gif) |
(40) |
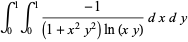 |
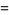 |
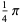 |
(41) |
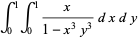 |
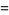 |
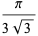 |
(42) |
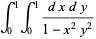 |
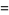 |
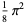 |
(43) |
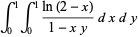 |
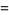 |
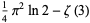 |
(44) |
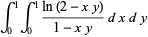 |
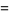 |
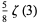 |
(45) |
 |
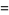 |
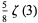 |
(46) |
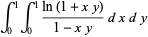 |
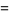 |
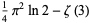 |
(47) |
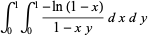 |
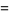 |
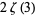 |
(48) |
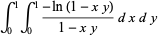 |
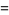 |
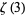 |
(49) |
![int_0^1int_0^1(xdxdy)/([-ln(xy)]^(3/2))](http://mathworld.wolfram.com/images/equations/UnitSquareIntegral/Inline161.gif) |
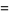 |
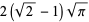 |
(50) |
![int_0^1int_0^1(dxdy)/([-ln(xy)]^(3/2))](http://mathworld.wolfram.com/images/equations/UnitSquareIntegral/Inline164.gif) |
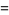 |
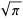 |
(51) |
![int_0^1int_0^1(dxdy)/([-ln(xy)]^(5/4))](http://mathworld.wolfram.com/images/equations/UnitSquareIntegral/Inline167.gif) |
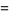 |
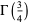 |
(52) |
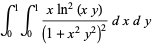 |
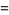 |
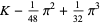 |
(53) |
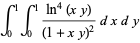 |
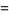 |
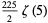 |
(54) |
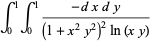 |
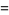 |
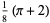 |
(55) |
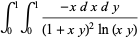 |
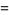 |
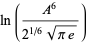 |
(56) |
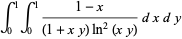 |
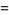 |
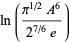 |
(57) |
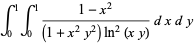 |
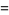 |
![ln[(Gamma(1/4))/(2Gamma(3/4))]+(2K)/pi-1/2](http://mathworld.wolfram.com/images/equations/UnitSquareIntegral/Inline187.gif) |
(58) |
![int_0^1int_0^1(1-x)/([-ln(xy)]^(5/2))dxdy](http://mathworld.wolfram.com/images/equations/UnitSquareIntegral/Inline188.gif) |
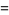 |
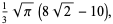 |
(59) |
where 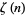 is the Riemann zeta function,
is the Riemann zeta function, 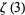 is Apéry's constant,
is Apéry's constant, 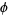 is the golden ratio,
is the golden ratio, 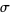 is Somos's quadratic recurrence constant, and
is Somos's quadratic recurrence constant, and 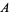 is the Glaisher-Kinkelin constant. Equation (57) appears in Sondow (2005), but is a special case of the type considered by Guillera and Sondow (2005).
is the Glaisher-Kinkelin constant. Equation (57) appears in Sondow (2005), but is a special case of the type considered by Guillera and Sondow (2005).
Corresponding single integrals over ![[0,1]](http://mathworld.wolfram.com/images/equations/UnitSquareIntegral/Inline196.gif) for most of these integrals can be found by making the change of variables
for most of these integrals can be found by making the change of variables 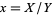 ,
, 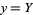 . The Jacobian then gives
. The Jacobian then gives 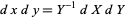 , and the new limits of integration are
, and the new limits of integration are {X,0,1}" src="http://mathworld.wolfram.com/images/equations/UnitSquareIntegral/Inline200.gif" style="height:14px; width:50px" />,
{Y,X,1}" src="http://mathworld.wolfram.com/images/equations/UnitSquareIntegral/Inline201.gif" style="height:14px; width:52px" />. Doing the integral with respect to
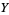 then gives a 1-dimensional integral over
then gives a 1-dimensional integral over ![[0,1]](http://mathworld.wolfram.com/images/equations/UnitSquareIntegral/Inline203.gif) . For details, see the first part of the proof of Guillera-Sondow's Theorem 3.1.
. For details, see the first part of the proof of Guillera-Sondow's Theorem 3.1.
REFERENCES:
Bailey, D. H.; Borwein, J. M.; Calkin, N. J.; Girgensohn, R.; Luke, D. R.; and Moll, V. H. Experimental Mathematics in Action. Wellesley, MA: A K Peters, 2007.
Beukers, F. "A Note on the Irrationality of 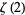 and
and 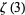 ." Bull. London Math. Soc. 11, 268-272, 1979.
." Bull. London Math. Soc. 11, 268-272, 1979.
Borwein, J.; Bailey, D.; and Girgensohn, R. Experimentation in Mathematics: Computational Paths to Discovery. Wellesley, MA: A K Peters, 2004.
Guillera, J. and Sondow, J. "Double Integrals and Infinite Products for Some Classical Constants Via Analytic Continuations of Lerch's Transcendent." 16 June 2005. http://arxiv.org/abs/math.NT/0506319.
Hadjicostas, P. "Some Generalizations of Beukers' Integrals." Kyungpook Math. J. 42, 399-416, 2002.
Sloane, N. J. A. Sequences A093753 and A093754 in "The On-Line Encyclopedia of Integer Sequences."
Sondow, J. "Criteria for Irrationality of Euler's Constant." Proc. Amer. Math. Soc. 131, 3335-3344, 2003. http://arxiv.org/abs/math.NT/0209070.
Sondow, J. "Double Integrals for Euler's Constant and 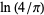 and an Analog of Hadjicostas's Formula." Amer. Math. Monthly 112, 61-65, 2005.
and an Analog of Hadjicostas's Formula." Amer. Math. Monthly 112, 61-65, 2005.
Zudilin, W. "An Apéry-Like Difference Equation for Catalan's Constant." Electronic J. Combinatorics 10, No. 1, R14, 1-10, 2003. http://www.combinatorics.org/Volume_10/Abstracts/v10i1r14.html.
 الاكثر قراءة في التفاضل و التكامل
الاكثر قراءة في التفاضل و التكامل
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















