

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Arithmetic-Geometric Mean
المؤلف:
Abramowitz, M. and Stegu"The Process of the Arithmetic-Geometric Mean." §17.6 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dovern, I. A.
المصدر:
"The Process of the Arithmetic-Geometric Mean." §17.6 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover
الجزء والصفحة:
...
17-3-2019
4076
Arithmetic-Geometric Mean
The arithmetic-geometric mean 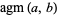 of two numbers
of two numbers 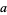 and
and 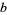 (often also written
(often also written 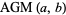 or
or 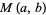 ) is defined by starting with
) is defined by starting with 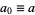 and
and 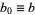 , then iterating
, then iterating
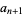 |
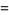 |
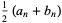 |
(1) |
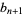 |
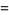 |
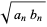 |
(2) |
until 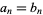 to the desired precision.
to the desired precision.
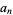 and
and 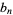 converge towards each other since
converge towards each other since
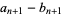 |
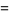 |
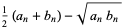 |
(3) |
 |
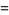 |
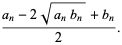 |
(4) |
But 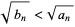 , so
, so
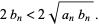 |
(5) |
Now, add 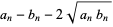 to each side
to each side
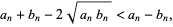 |
(6) |
so
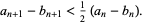 |
(7) |
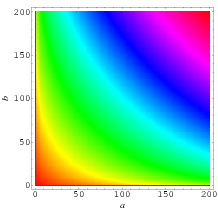 |
 |
The top plots show 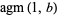 for
for 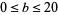 and
and 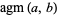 for
for 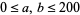 , while the bottom two plots show
, while the bottom two plots show 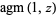 for complex values of
for complex values of 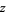 .
.
The AGM is very useful in computing the values of complete elliptic integrals and can also be used for finding the inverse tangent.
It is implemented in the Wolfram Language as ArithmeticGeometricMean[a, b].
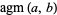 can be expressed in closed form in terms of the complete elliptic integral of the first kind
can be expressed in closed form in terms of the complete elliptic integral of the first kind 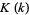 as
as
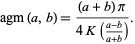 |
(8) |
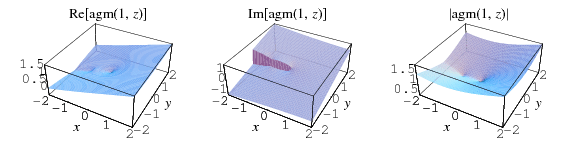
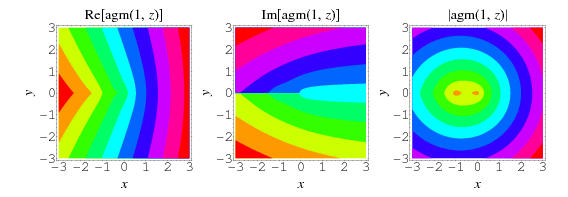
The definition of the arithmetic-geometric mean also holds in the complex plane, as illustrated above for 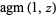 .
.
The Legendre form of the arithmetic-geometric mean is given by
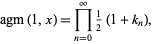 |
(9) |
where 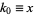 and
and
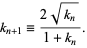 |
(10) |
Special values of 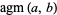 are summarized in the following table. The special value
are summarized in the following table. The special value
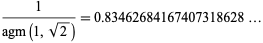 |
(11) |
(OEIS A014549) is called Gauss's constant. It has the closed form
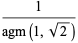 |
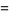 |
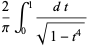 |
(12) |
 |
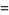 |
![([Gamma(1/4)]^2)/(2pi^(3/2)sqrt(2))](http://mathworld.wolfram.com/images/equations/Arithmetic-GeometricMean/Inline41.gif) |
(13) |
where the above integral is the lemniscate function and the equality of the arithmetic-geometric mean to this integral was known to Gauss (Borwein and Bailey 2003, pp. 13-15).
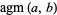 |
Sloane | value |
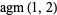 |
A068521 | 1.4567910310469068692... |
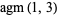 |
A084895 | 1.8636167832448965424... |
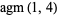 |
A084896 | 2.2430285802876025701... |
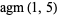 |
A084897 | 2.6040081905309402887... |
The derivative of the AGM is given by
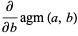 |
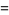 |
![(agm(a,b))/((a-b)bpi)[2agm(a,b)E(k)-bpi]](http://mathworld.wolfram.com/images/equations/Arithmetic-GeometricMean/Inline49.gif) |
(14) |
 |
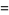 |
![pi/(8kb)((a+b)E(k)-2bK(k))/([K(k)]^2),](http://mathworld.wolfram.com/images/equations/Arithmetic-GeometricMean/Inline52.gif) |
(15) |
where 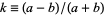 ,
, 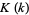 is a complete elliptic integral of the first kind, and
is a complete elliptic integral of the first kind, and 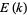 is the complete elliptic integral of the second kind.
is the complete elliptic integral of the second kind.
A series expansion for 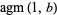 is given by
is given by
![agm(1,b)=-pi/(2ln(1/4b))+(pi[1+ln(1/4b)]b^2)/(8[ln(1/4b)]^2)+O(b^4).](http://mathworld.wolfram.com/images/equations/Arithmetic-GeometricMean/NumberedEquation8.gif) |
(16) |
The AGM has the properties
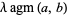 |
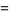 |
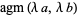 |
(17) |
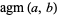 |
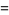 |
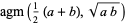 |
(18) |
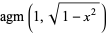 |
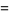 |
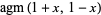 |
(19) |
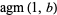 |
 |
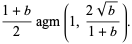 |
(20) |
Solutions to the differential equation
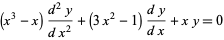 |
(21) |
are given by ![[agm(1+x,1-x)]^(-1)](http://mathworld.wolfram.com/images/equations/Arithmetic-GeometricMean/Inline69.gif) and
and ![[agm(1,x)]^(-1)](http://mathworld.wolfram.com/images/equations/Arithmetic-GeometricMean/Inline70.gif) .
.
A generalization of the arithmetic-geometric mean is
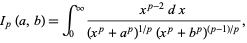 |
(22) |
which is related to solutions of the differential equation
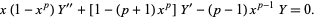 |
(23) |
The case 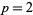 corresponds to the arithmetic-geometric mean via
corresponds to the arithmetic-geometric mean via
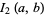 |
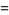 |
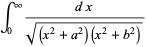 |
(24) |
 |
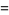 |
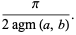 |
(25) |
The case 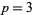 gives the cubic relative
gives the cubic relative
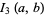 |
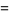 |
![int_0^infty(xdx)/([(a^3+x^3)(b^3+x^3)^2]^(1/3))](http://mathworld.wolfram.com/images/equations/Arithmetic-GeometricMean/Inline81.gif) |
(26) |
 |
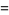 |
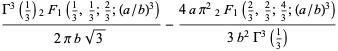 |
(27) |
discussed by Borwein and Borwein (1990, 1991) and Borwein (1996). For 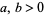 , this function satisfies the functional equation
, this function satisfies the functional equation
![I_3(a,b)=I_3((a+2b)/3,[b/3(a^2+ab+b^2)]^(1/3)).](http://mathworld.wolfram.com/images/equations/Arithmetic-GeometricMean/NumberedEquation12.gif) |
(28) |
It therefore turns out that for iteration with 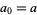 and
and 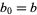 and
and
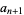 |
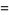 |
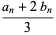 |
(29) |
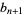 |
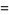 |
![[(b_n)/3(a_n^2+a_nb_n+b_n^2)]^(1/3),](http://mathworld.wolfram.com/images/equations/Arithmetic-GeometricMean/Inline93.gif) |
(30) |
so
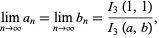 |
(31) |
where
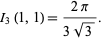 |
(32) |
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). "The Process of the Arithmetic-Geometric Mean." §17.6 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 571 and 598-599, 1972.
Borwein, J. and Bailey, D. Mathematics by Experiment: Plausible Reasoning in the 21st Century. Wellesley, MA: A K Peters, 2003.
Borwein, J. M. Problem 10281. "A Cubic Relative of the AGM." Amer. Math. Monthly 103, 181-183, 1996.
Borwein, J. M. and Borwein, P. B. Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity. New York: Wiley, 1987.
Borwein, J. M. and Borwein, P. B. "A Remarkable Cubic Iteration." In Computational Method & Function Theory: Proc. Conference Held in Valparaiso, Chile, March 13-18, 1989 (Ed. A. Dold, B. Eckmann, F. Takens, E. B. Saff, S. Ruscheweyh, L. C. Salinas, and R. S. Varga). New York: Springer-Verlag, 1990.
Borwein, J. M. and Borwein, P. B. "A Cubic Counterpart of Jacobi's Identity and the AGM." Trans. Amer. Math. Soc. 323, 691-701, 1991.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 906-907, 1992.
Sloane, N. J. A. Sequences A014549, A068521, A084895, A084896, and A084897 in "The On-Line Encyclopedia of Integer Sequences."
 الاكثر قراءة في التفاضل و التكامل
الاكثر قراءة في التفاضل و التكامل
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















