
Airy-Fock Functions
 المؤلف:
Babich, V. M. and Kirpichnikova, N.
المؤلف:
Babich, V. M. and Kirpichnikova, N.
 المصدر:
The Boundary Layer Method in Diffraction Problems. New York: Springer-Verlag, 1979.
المصدر:
The Boundary Layer Method in Diffraction Problems. New York: Springer-Verlag, 1979.
 الجزء والصفحة:
...
الجزء والصفحة:
...
 24-3-2019
24-3-2019
 1831
1831
Airy-Fock Functions
Fok (1946) and Hazewinkel (1988, p. 65) call
where 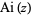 is an Airy function and
is an Airy function and 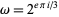 , the Airy-Fock functions.
, the Airy-Fock functions.
On the other hand, Fock (1965) and Kiselev et al. (2003) and Babich and Buldyrev (2008) use the notation 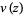 to denote twice the quantity
to denote twice the quantity 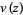 in equation (1), and term this function (alone) "the Airy-Fock function."
in equation (1), and term this function (alone) "the Airy-Fock function."
These three functions satisfy
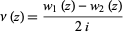 |
(4)
|
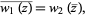 |
(5)
|
where 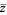 is the complex conjugate of
is the complex conjugate of 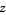 .
.
REFERENCES:
Babich, V. M. and Kirpichnikova, N. Ya. The Boundary Layer Method in Diffraction Problems. New York: Springer-Verlag, 1979.
Babich, M. and Buldyrev, V. S. Asymptotic Methods in Short-Wavelength Diffraction Theory. Alpha Science, 2008.
Fock, V. A. Electromagnetic Diffraction and Propagation Problems. Oxford, England: Pergamon Press, 1965.
Fok, V. A. Tables of Airy Functions. Moscow, 1946.
Hazewinkel, M. (Managing Ed.). Encyclopaedia of Mathematics: An Updated and Annotated Translation of the Soviet "Mathematical Encyclopaedia." Dordrecht, Netherlands: Reidel, p. 65, 1988.
Kiselev, A. P.; Yarovoĭ, V. O.; and Vsemirnova, E. A. "Polarization Anomalies of Elastic Waves. Caustic and Penumbra." Zap. Nauchn. Sem. St.-Petersburg. Otdel. Mat. Inst. Steklov. (POMI) 297, 2003. Published in Mat. Vopr. Teor. Rasprostr. Voln. 32, 136-153 and 275-27. Translation in J. Math. Sci. (N. Y.) 127, 2413-2423, 2005.
 الاكثر قراءة في التفاضل و التكامل
الاكثر قراءة في التفاضل و التكامل
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


