Inverse Erf
المؤلف:
Bergeron, F.; Labelle, G.; and Leroux, P
المصدر:
Ch. 5 in Combinatorial Species and Tree-Like Structures. Cambridge, England: Cambridge University Press, 1998.
الجزء والصفحة:
...
28-4-2019
1630
Inverse Erf
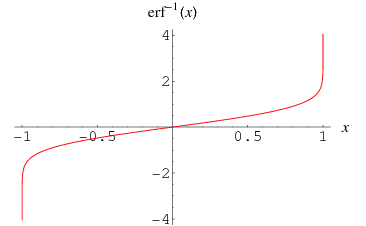
The inverse erf function is the inverse function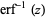 
of the erf function 
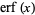such that
with the first identity holding for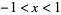 
and the second for 
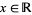. It is implemented in the Wolfram Language as InverseErf[x].
It is an odd function since
 |
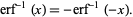(3)
|
It has the special values
It is apparently not known if
 |
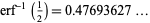(7)
|
(OEIS A069286) can be written in closed form.
It satisfies the equation
 |
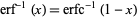(8)
|
where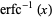 
is the inverse erfc function.
It has the derivative
![d/(dx)erf^(-1)(x)=1/2sqrt(pi)e^([erf^(-1)(x)]^2),](http://mathworld.wolfram.com/images/equations/InverseErf/NumberedEquation4.gif) |
(9)
|
and its integral is
![interf^(-1)(x)dx=-(e^(-[erf^(-1)(x)]^2))/(sqrt(pi))](http://mathworld.wolfram.com/images/equations/InverseErf/NumberedEquation5.gif) |
(10)
|
(which follows from the method of Parker 1955).
Definite integrals are given by
(OEIS A087197 and A114864), where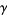 
is the Euler-Mascheroni constant and 
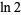is the natural logarithm of 2.
The Maclaurin series of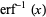 
is given by
 |
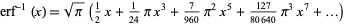(15)
|
(OEIS A002067 and A007019). Written in simplified form so that the coefficient of 
is 1,
 |
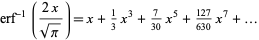(16)
|
(OEIS A092676 and A092677). The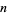 
th coefficient of this series can be computed as
 |
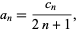(17)
|
where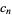 
is given by the recurrence equation
 |
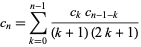(18)
|
with initial condition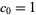 
.
REFERENCES:
Bergeron, F.; Labelle, G.; and Leroux, P. Ch. 5 in Combinatorial Species and Tree-Like Structures. Cambridge, England: Cambridge University Press, 1998.
Carlitz, L. "The Inverse of the Error Function." Pacific J. Math. 13, 459-470, 1963.
Parker, F. D. "Integrals of Inverse Functions." Amer. Math. Monthly 62, 439-440, 1955.
Sloane, N. J. A. Sequences A002067/M4458, A007019/M3126, A069286, A087197, A092676, A092677, A114859, A114860, and A114864 in "The On-Line Encyclopedia of Integer Sequences."
الاكثر قراءة في التفاضل و التكامل
اخر الاخبار
اخبار العتبة العباسية المقدسة
