Subfactorial
The 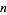 th subfactorial (also called the derangement number; Goulden and Jackson 1983, p. 48; Graham et al. 2003, p. 1050) is the number of permutations of
th subfactorial (also called the derangement number; Goulden and Jackson 1983, p. 48; Graham et al. 2003, p. 1050) is the number of permutations of 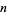 objects in which no object appears in its natural place (i.e., "derangements").
objects in which no object appears in its natural place (i.e., "derangements").
The term "subfactorial "was introduced by Whitworth (1867 or 1878; Cajori 1993, p. 77). Euler (1809) calculated the first ten terms.
The first few values of 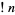 for
for 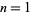 , 2, ... are 0, 1, 2, 9, 44, 265, 1854, 14833, ... (OEIS A000166). For example, the only derangements of
, 2, ... are 0, 1, 2, 9, 44, 265, 1854, 14833, ... (OEIS A000166). For example, the only derangements of ![<span style=]() {1,2,3}" src="http://mathworld.wolfram.com/images/equations/Subfactorial/Inline5.gif" style="height:14px; width:47px" /> are
{1,2,3}" src="http://mathworld.wolfram.com/images/equations/Subfactorial/Inline5.gif" style="height:14px; width:47px" /> are ![<span style=]() {2,3,1}" src="http://mathworld.wolfram.com/images/equations/Subfactorial/Inline6.gif" style="height:14px; width:47px" /> and
{2,3,1}" src="http://mathworld.wolfram.com/images/equations/Subfactorial/Inline6.gif" style="height:14px; width:47px" /> and ![<span style=]() {3,1,2}" src="http://mathworld.wolfram.com/images/equations/Subfactorial/Inline7.gif" style="height:14px; width:47px" />, so
{3,1,2}" src="http://mathworld.wolfram.com/images/equations/Subfactorial/Inline7.gif" style="height:14px; width:47px" />, so 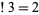 . Similarly, the derangements of
. Similarly, the derangements of ![<span style=]() {1,2,3,4}" src="http://mathworld.wolfram.com/images/equations/Subfactorial/Inline9.gif" style="height:14px; width:62px" /> are
{1,2,3,4}" src="http://mathworld.wolfram.com/images/equations/Subfactorial/Inline9.gif" style="height:14px; width:62px" /> are ![<span style=]() {2,1,4,3}" src="http://mathworld.wolfram.com/images/equations/Subfactorial/Inline10.gif" style="height:14px; width:62px" />,
{2,1,4,3}" src="http://mathworld.wolfram.com/images/equations/Subfactorial/Inline10.gif" style="height:14px; width:62px" />, ![<span style=]() {2,3,4,1}" src="http://mathworld.wolfram.com/images/equations/Subfactorial/Inline11.gif" style="height:14px; width:62px" />,
{2,3,4,1}" src="http://mathworld.wolfram.com/images/equations/Subfactorial/Inline11.gif" style="height:14px; width:62px" />, ![<span style=]() {2,4,1,3}" src="http://mathworld.wolfram.com/images/equations/Subfactorial/Inline12.gif" style="height:14px; width:62px" />,
{2,4,1,3}" src="http://mathworld.wolfram.com/images/equations/Subfactorial/Inline12.gif" style="height:14px; width:62px" />, ![<span style=]() {3,1,4,2}" src="http://mathworld.wolfram.com/images/equations/Subfactorial/Inline13.gif" style="height:14px; width:62px" />,
{3,1,4,2}" src="http://mathworld.wolfram.com/images/equations/Subfactorial/Inline13.gif" style="height:14px; width:62px" />, ![<span style=]() {3,4,1,2}" src="http://mathworld.wolfram.com/images/equations/Subfactorial/Inline14.gif" style="height:14px; width:62px" />,
{3,4,1,2}" src="http://mathworld.wolfram.com/images/equations/Subfactorial/Inline14.gif" style="height:14px; width:62px" />, ![<span style=]() {3,4,2,1}" src="http://mathworld.wolfram.com/images/equations/Subfactorial/Inline15.gif" style="height:14px; width:62px" />,
{3,4,2,1}" src="http://mathworld.wolfram.com/images/equations/Subfactorial/Inline15.gif" style="height:14px; width:62px" />, ![<span style=]() {4,1,2,3}" src="http://mathworld.wolfram.com/images/equations/Subfactorial/Inline16.gif" style="height:14px; width:62px" />,
{4,1,2,3}" src="http://mathworld.wolfram.com/images/equations/Subfactorial/Inline16.gif" style="height:14px; width:62px" />, ![<span style=]() {4,3,1,2}" src="http://mathworld.wolfram.com/images/equations/Subfactorial/Inline17.gif" style="height:14px; width:62px" />, and
{4,3,1,2}" src="http://mathworld.wolfram.com/images/equations/Subfactorial/Inline17.gif" style="height:14px; width:62px" />, and ![<span style=]() {4,3,2,1}" src="http://mathworld.wolfram.com/images/equations/Subfactorial/Inline18.gif" style="height:14px; width:62px" />, so
{4,3,2,1}" src="http://mathworld.wolfram.com/images/equations/Subfactorial/Inline18.gif" style="height:14px; width:62px" />, so 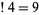 .
.
Sums and formulas for 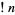 include
include
where 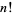 is a factorial,
is a factorial, 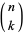 is a binomial coefficient, and
is a binomial coefficient, and 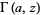 is the incomplete gamma function.
is the incomplete gamma function.
Subfactorials are implemented in the Wolfram Language as Subfactorial[n].
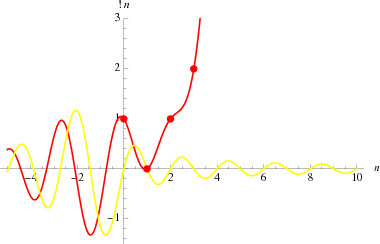
A plot the real and imaginary parts of the subfactorial generalized to any real argument is illustrated above, with the usual integer-valued subfactorial corresponding to nonnegative integer 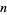 .
.
The subfactorials are also called the rencontres numbers and satisfy the recurrence relations
The subfactorial can be considered a special case of a restricted rooks problem.
The subfactorial has generating function
where 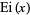 is the exponential integral, and exponential generating function
is the exponential integral, and exponential generating function
(OEIS A053557 and A053556).
Subfactorials are commonly denoted 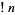 ,
, 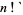 (Graham et al. 2003, p. 194),
(Graham et al. 2003, p. 194), 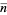 (Dörrie 1965, p. 19),
(Dörrie 1965, p. 19), 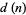 (Pemmaraju and Skiena 2003, p. 106),
(Pemmaraju and Skiena 2003, p. 106), 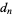 (Goulden and Jackson 1983, p. 48; van Lint and Wilson 1992, p. 90), or
(Goulden and Jackson 1983, p. 48; van Lint and Wilson 1992, p. 90), or 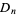 (Riordan 1980, p. 59; Stanley 1997, p. 489), the latter being especially used when viewing them as derangements.
(Riordan 1980, p. 59; Stanley 1997, p. 489), the latter being especially used when viewing them as derangements.
Another equation is given by
![!n=[(n!)/e],](http://mathworld.wolfram.com/images/equations/Subfactorial/NumberedEquation1.gif) |
(13)
|
where 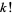 is the usual factorial and
is the usual factorial and ![[x]](http://mathworld.wolfram.com/images/equations/Subfactorial/Inline69.gif) is the nearest integer function. M. Hassani (pers. comm., Oct. 28, 2004) gave the forms
is the nearest integer function. M. Hassani (pers. comm., Oct. 28, 2004) gave the forms
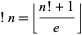 |
(14)
|
for 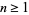 and
and
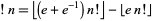 |
(15)
|
for 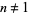 , where
, where 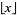 is the floor function.
is the floor function.
An integral for 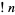 is given by
is given by
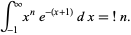 |
(16)
|
A continued fraction for 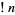 is given by
is given by
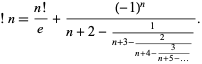 |
(17)
|
The numbers of decimal digits in 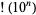 for
for 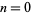 , 1, ... are 7, 158, 2568, 35660, 456574, 5565709, 65657059, ... (OEIS A114485).
, 1, ... are 7, 158, 2568, 35660, 456574, 5565709, 65657059, ... (OEIS A114485).
The only prime subfactorial is 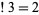 .
.
The only number equal to the sum of subfactorials of its digits is
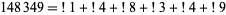 |
(18)
|
(Madachy 1979).
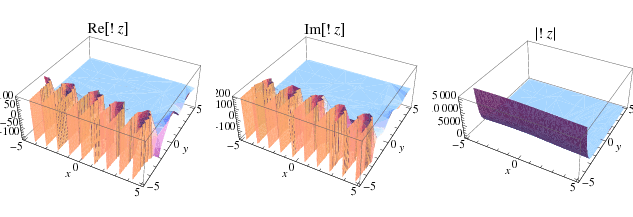
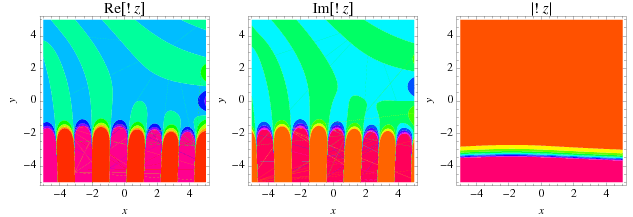
The subfactorial may be analytically continued to the complex plane, as illustrated above.
REFERENCES:
Cajori, F. A History of Mathematical Notations, Vol. 2. New York: Cosimo Classics, 2007.
Dörrie, H. §6 in 100 Great Problems of Elementary Mathematics: Their History and Solutions. New York: Dover, pp. 19-21, 1965.
Euler, L. "Solution quaestionis curiosae ex doctrina combinationum." Mémoires Académie Sciences St. Pétersbourg 3, 57-64, 1809. Reprinted in Opera Omnia, Series Prima, Vol. 7. Leipzig, Germany: Teubner, pp. 435-440, 1915.
Goulden, I. P. and Jackson, D. M. Combinatorial Enumeration. New York: Wiley, 1983.
Graham, R. L.; Grötschel, M.; and Lovász, L. (Eds.). Handbook of Combinatorics, Vol. 2. Cambridge, MA: MIT Press, 2003.
Madachy, J. S. Madachy's Mathematical Recreations. New York: Dover, p. 167, 1979.
Pemmaraju, S. and Skiena, S. Computational Discrete Mathematics: Combinatorics and Graph Theory with Mathematica.Cambridge, England: Cambridge University Press, 2003.
Riordan, J. An Introduction to Combinatorial Analysis. New York: Wiley, 1980.
Sloane, N. J. A. Sequences A000166/M1937, A053556, A053557, and A114485 in "The On-Line Encyclopedia of Integer Sequences."
Sloane, N. J. A. and Plouffe, S. Figure M1937 in The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.
Stanley, R. P. Enumerative Combinatorics, Vol. 1. Cambridge, England: Cambridge University Press, p. 67, 1997.
van Lint, J. H. and Wilson, R. M. A Course in Combinatorics. New York: Cambridge University Press, 1992.
Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, p. 27, 1986.
Whitworth, W. A. Choice and Chance, Two Chapters of Arithmetic, with an Appendix Containing the Algebraical Treatment of Permutations and Combinations Newly Set Forth. Cambridge, England: Deighton, Bell, 1867.
Whitworth, W. A. Messenger Math. 1878.
 الاكثر قراءة في التفاضل و التكامل
الاكثر قراءة في التفاضل و التكامل
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


