Bohr-Mollerup Theorem
المؤلف:
Havil, J.
المصدر:
Gamma: Exploring Euler,s Constant. Princeton, NJ: Princeton University Press
الجزء والصفحة:
...
21-5-2019
2186
Bohr-Mollerup Theorem
If a function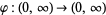 
satisfies
1. ![ln[phi(x)]](http://mathworld.wolfram.com/images/equations/Bohr-MollerupTheorem/Inline2.gif)
is convex,
2. 
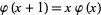for all 
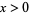, and
3. 
,
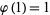then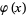 
is the gamma function 
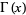. Therefore, by analytic continuation, 
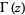is the only meromorphic function on 
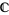satisfying the functional equation
with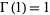 
and which is logarithmically convex on the positive real axis.
REFERENCES:
Havil, J. Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, pp. 56-57, 2003.
Krantz, S. G. "The Bohr-Mollerup Theorem." §13.1.10 in Handbook of Complex Variables. Boston, MA: Birkhäuser, p. 157, 1999.
الاكثر قراءة في التفاضل و التكامل
اخر الاخبار
اخبار العتبة العباسية المقدسة
