Meijer G-Function
The Meijer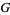 
-function is a very general function which reduces to simpler special functions in many common cases. The Meijer 
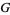-function is defined by
 |
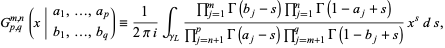(1)
|
where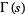 
is the gamma function (Erdélyi et al. 1981, p. 1068; Gradshteyn and Ryzhik 2000). A different but equivalent form is used by Prudnikov et al. (1990, p. 793),
 |
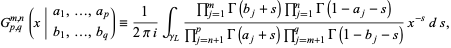(2)
|
This form provides more consistency with the definition of this function via an inverse Mellin transform.
The Meijer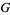 
-function is implemented in the Wolfram Language as MeijerG[![<span style=]()
{" src="http://mathworld.wolfram.com/images/equations/MeijerG-Function/Inline5.gif" style="height:14px; width:5px" />![<span style=]()
{" src="http://mathworld.wolfram.com/images/equations/MeijerG-Function/Inline6.gif" style="height:14px; width:5px" />a1, ..., an![<span style=]()
}" src="http://mathworld.wolfram.com/images/equations/MeijerG-Function/Inline7.gif" style="height:14px; width:5px" />, ![<span style=]()
{" src="http://mathworld.wolfram.com/images/equations/MeijerG-Function/Inline8.gif" style="height:14px; width:5px" />a(n+1), ..., ap![<span style=]()
}" src="http://mathworld.wolfram.com/images/equations/MeijerG-Function/Inline9.gif" style="height:14px; width:5px" />![<span style=]()
}" src="http://mathworld.wolfram.com/images/equations/MeijerG-Function/Inline10.gif" style="height:14px; width:5px" />, ![<span style=]()
{" src="http://mathworld.wolfram.com/images/equations/MeijerG-Function/Inline11.gif" style="height:14px; width:5px" />![<span style=]()
{" src="http://mathworld.wolfram.com/images/equations/MeijerG-Function/Inline12.gif" style="height:14px; width:5px" />b1, ..., bm![<span style=]()
}" src="http://mathworld.wolfram.com/images/equations/MeijerG-Function/Inline13.gif" style="height:14px; width:5px" />, ![<span style=]()
{" src="http://mathworld.wolfram.com/images/equations/MeijerG-Function/Inline14.gif" style="height:14px; width:5px" />b(m+1), ..., bq![<span style=]()
}" src="http://mathworld.wolfram.com/images/equations/MeijerG-Function/Inline15.gif" style="height:14px; width:5px" />![<span style=]()
}" src="http://mathworld.wolfram.com/images/equations/MeijerG-Function/Inline16.gif" style="height:14px; width:5px" />, z]. A generalized form of the function defined by
 |
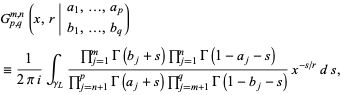(3)
|
is implemented in the Wolfram Language as MeijerG[![<span style=]()
{" src="http://mathworld.wolfram.com/images/equations/MeijerG-Function/Inline17.gif" style="height:14px; width:5px" />![<span style=]()
{" src="http://mathworld.wolfram.com/images/equations/MeijerG-Function/Inline18.gif" style="height:14px; width:5px" />a1, ..., an![<span style=]()
}" src="http://mathworld.wolfram.com/images/equations/MeijerG-Function/Inline19.gif" style="height:14px; width:5px" />, ![<span style=]()
{" src="http://mathworld.wolfram.com/images/equations/MeijerG-Function/Inline20.gif" style="height:14px; width:5px" />a(n+1), ..., ap![<span style=]()
}" src="http://mathworld.wolfram.com/images/equations/MeijerG-Function/Inline21.gif" style="height:14px; width:5px" />![<span style=]()
}" src="http://mathworld.wolfram.com/images/equations/MeijerG-Function/Inline22.gif" style="height:14px; width:5px" />, ![<span style=]()
{" src="http://mathworld.wolfram.com/images/equations/MeijerG-Function/Inline23.gif" style="height:14px; width:5px" />![<span style=]()
{" src="http://mathworld.wolfram.com/images/equations/MeijerG-Function/Inline24.gif" style="height:14px; width:5px" />b1, ..., bm![<span style=]()
}" src="http://mathworld.wolfram.com/images/equations/MeijerG-Function/Inline25.gif" style="height:14px; width:5px" />, ![<span style=]()
{" src="http://mathworld.wolfram.com/images/equations/MeijerG-Function/Inline26.gif" style="height:14px; width:5px" />b(m+1), ..., bq![<span style=]()
}" src="http://mathworld.wolfram.com/images/equations/MeijerG-Function/Inline27.gif" style="height:14px; width:5px" />![<span style=]()
}" src="http://mathworld.wolfram.com/images/equations/MeijerG-Function/Inline28.gif" style="height:14px; width:5px" />, z, r].
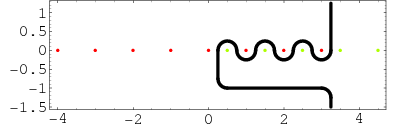
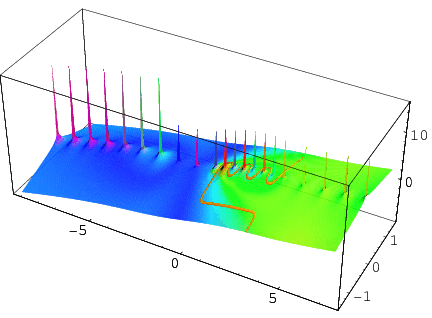
In both (2) and (3), the contour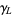 
lies between the poles of 
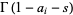and the poles of 
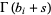. For example, the contour for 
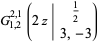is illustrated above, both in the complex plane and superposed on the function itself (M. Trott).
Prudnikov et al. (1990) contains an extensive nearly 200-page listing of formulas for the Meijer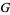 
-function.
Special cases include
A special case of the 2-argument form is
 |
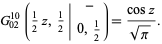(8)
|
REFERENCES:
Adamchik, V. "The Evaluation of Integrals of Bessel Functions via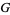 
-Function Identities." J. Comput. Appl. Math. 64, 283-290, 1995.
Erdélyi, A.; Magnus, W.; Oberhettinger, F.; and Tricomi, F. G. "Definition of the G-Function" et seq. §5.3-5.6 in Higher Transcendental Functions, Vol. 1. New York: Krieger, pp. 206-222, 1981.
Gradshteyn, I. S. and Ryzhik, I. M. "Meijer's and MacRobert's Function (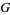
and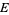 
)" and "Meijer's 
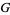-Function." §7.8 and 9.3 in Tables of Integrals, Series, and Products, 6th ed. San Diego, CA: Academic Press, pp. 843-850 and 1022-1025, 2000.
Luke, Y. L. The Special Functions and Their Approximations, 2 vols. New York: Academic Press, 1969.
Mathai, A. M. A Handbook of Generalized Special Functions for Statistical and Physical Sciences. New York: Oxford University Press, 1993.
Meijer, C. S. "Multiplikationstheoreme für di Funktion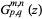 
." Proc. Nederl. Akad. Wetensch. 44, 1062-1070, 1941.
Meijer, C. S. "On the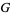 
-Function. II." Proc. Nederl. Akad. Wetensch. 49, 344-456, 1946.
Meijer, C. S. "On the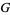 
-Function. III." Proc. Nederl. Akad. Wetensch. 49, 457-469, 1946.
Meijer, C. S. "On the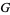 
-Function. IV." Proc. Nederl. Akad. Wetensch. 49, 632-641, 1946.
Meijer, C. S. "On the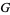 
-Function. V." Proc. Nederl. Akad. Wetensch. 49, 765-772, 1946.
Meijer, C. S. "On the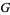 
-Function. VI." Proc. Nederl. Akad. Wetensch. 49, 936-943, 1946.
Meijer, C. S. "On the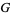 
-Function. VII." Proc. Nederl. Akad. Wetensch. 49, 1063-1072, 1946.
Meijer, C. S. "On the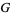 
-Function. VIII." Proc. Nederl. Akad. Wetensch. 49, 1165-1175, 1946.
Prudnikov, A. P.; Brychkov, Yu. A.; and Marichev, O. I. "Evaluation of Integrals and the Mellin Transform." Itogi Nauki i Tekhniki, Seriya Matemat. Analiz 27, 3-146, 1989.
Prudnikov, A. P.; Marichev, O. I.; and Brychkov, Yu. A. "The Meijer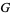 
-Function 
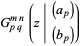." §8.2 in Integrals and Series, Vol. 3: More Special Functions. Newark, NJ: Gordon and Breach, pp. 617-626, 1990.
الاكثر قراءة في التفاضل و التكامل
اخر الاخبار
اخبار العتبة العباسية المقدسة
