


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 22-5-2019
Date: 25-5-2019
Date: 10-6-2019
|
![(d^2V)/(dv^2)+[a-2qcos(2v)]V=0](http://mathworld.wolfram.com/images/equations/MathieuDifferentialEquation/NumberedEquation1.gif) |
(1) |
(Abramowitz and Stegun 1972; Zwillinger 1997, p. 125), having solution
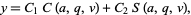 |
(2) |
where 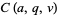 and
and 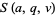 are Mathieu functions. The equation arises in separation of variables of the Helmholtz differential equation in elliptic cylindrical coordinates. Whittaker and Watson (1990) use a slightly different form to define the Mathieu functions.
are Mathieu functions. The equation arises in separation of variables of the Helmholtz differential equation in elliptic cylindrical coordinates. Whittaker and Watson (1990) use a slightly different form to define the Mathieu functions.
The modified Mathieu differential equation
![(d^2U)/(du^2)-[a-2qcosh(2u)]U=0](http://mathworld.wolfram.com/images/equations/MathieuDifferentialEquation/NumberedEquation3.gif) |
(3) |
(Iyanaga and Kawada 1980, p. 847; Zwillinger 1997, p. 125) arises in separation of variables of the Helmholtz differential equation in elliptic cylindrical coordinates, and has solutions
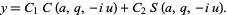 |
(4) |
The associated Mathieu differential equation is given by
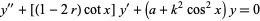 |
(5) |
(Ince 1956, p. 403; Zwillinger 1997, p. 125).
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 722, 1972.
Campbell, R. Théorie générale de l'équation de Mathieu et de quelques autres équations différentielles de la mécanique. Paris: Masson, 1955.
Ince, E. L. Ordinary Differential Equations. New York: Dover, 1956.
Iyanaga, S. and Kawada, Y. (Eds.). Encyclopedic Dictionary of Mathematics. Cambridge, MA: MIT Press, p. 847, 1980.
Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 556-557, 1953.
Whittaker, E. T. and Watson, G. N. A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge University Press, 1990.
Zwillinger, D. (Ed.). CRC Standard Mathematical Tables and Formulae. Boca Raton, FL: CRC Press, 1995.
Zwillinger, D. Handbook of Differential Equations, 3rd ed. Boston, MA: Academic Press, p. 125, 1997.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
عقد جلسة حوارية عن ضحايا جرائم التطرف ضمن فعاليات اليوم الثاني لمؤتمر ذاكرة الألم
|
|
|