Gauss's Digamma Theorem

At rational arguments 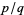, the digamma function  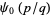is given by

(1)

for 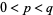 (Knuth 1997, p. 94). These give the special values

			(2)
			(3)
			(4)
			(5)
			(6)
			(7)
			(8)
			(9)

where 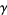 is the Euler-Mascheroni constant.

REFERENCES:

Allouche, J.-P. "Series and Infinite Products related to Binary Expansions of Integers." 1992. http://algo.inria.fr/seminars/sem92-93/allouche.ps.

Böhmer, E. Differenzengleichungen und bestimmte Integrale. Leipzig, Germany: Teubner, p. 77, 1939.

Erdélyi, A.; Magnus, W.; Oberhettinger, F.; and Tricomi, F. G. "The 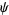 Function." §1.7 in Higher Transcendental Functions, Vol. 1. New York: Krieger, pp. 15-20, 1981.

Gradshteyn, I. S. and Ryzhik, I. M. Formula 8.3636 in Tables of Integrals, Series, and Products, 6th ed. San Diego, CA: Academic Press, 2000.

Jensen, J. L. W. V. "An Elementary Exposition of the Theory of the Gamma Function." Ann. Math. 17, 124-166, 1915.

Knuth, D. E. The Art of Computer Programming, Vol. 1: Fundamental Algorithms, 3rd ed. Reading, MA: Addison-Wesley, 1997.

Kölbig, K. S. "The Polygamma Function and the Derivatives of the Cotangent Function for Rational Arguments." Report CN/96/5. CERN Computing and Networks Division, 1996.

Lösch, F. and Schoblik, F. Die Fakultät und verwandte Funktionen. Leipzig, Germany: Teubner, p. 12, 1951.