
Jacobi Identities
 المؤلف:
Borwein, J. M. and Borwein, P. B
المؤلف:
Borwein, J. M. and Borwein, P. B
 المصدر:
Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity. New York: Wiley, 1987.
المصدر:
Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity. New York: Wiley, 1987.
 الجزء والصفحة:
...
الجزء والصفحة:
...
 25-8-2019
25-8-2019
 1557
1557
Jacobi Identities
"The" Jacobi identity is a relationship
![[A,[B,C]]+[B,[C,A]]+[C,[A,B]]=0,,](http://mathworld.wolfram.com/images/equations/JacobiIdentities/NumberedEquation1.gif) |
(1)
|
between three elements 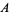 ,
, 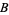 , and
, and 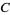 , where
, where ![[A,B]](http://mathworld.wolfram.com/images/equations/JacobiIdentities/Inline4.gif) is the commutator. The elements of a Lie algebra satisfy this identity.
is the commutator. The elements of a Lie algebra satisfy this identity.
Relationships between the Q-functions 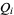 are also known as Jacobi identities:
are also known as Jacobi identities:
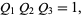 |
(2)
|
equivalent to the Jacobi triple product (Borwein and Borwein 1987, p. 65) and
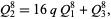 |
(3)
|
where
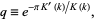 |
(4)
|
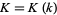 is the complete elliptic integral of the first kind, and
is the complete elliptic integral of the first kind, and 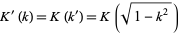 . Using Weber functions
. Using Weber functions
(5) and (6) become
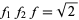 |
(8)
|
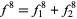 |
(9)
|
(Borwein and Borwein 1987, p. 69).
REFERENCES:
Borwein, J. M. and Borwein, P. B. Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity. New York: Wiley, 1987.
Hardy, G. H. and Wright, E. M. An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, 1979.
Schafer, R. D. An Introduction to Nonassociative Algebras. New York: Dover, p. 3, 1996.
 الاكثر قراءة في التفاضل و التكامل
الاكثر قراءة في التفاضل و التكامل
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


