A 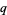-analog, also called a 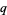-extension or 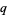-generalization, is a mathematical expression parameterized by a quantity  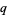that generalizes a known expression and reduces to the known expression in the limit 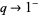. There are 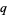-analogs of the factorial, binomial coefficient, derivative, integral, Fibonacci numbers, and so on. Koornwinder, Suslov, and Bustoz, have even managed some kind of 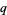-Fourier analysis. Note that while European writers generally prefer the British spelling "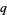-analogue" (Koekoek and Swarttouw 1998, p. 7; Koepf 1998, p. 26), American authors prefer the shorter "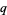-analog" (Andrews et al. 1999, pp. 490 and 496). To avoid this ambiguity (as well as the pitfall that there are sometimes more than just a single 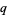-analog), the term 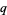-extension (Andrews et al. 1999, pp. 483, 485, 487, etc.) may be preferable.

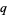-analogs are based on the observation that

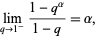(1)

and the quantity 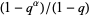 is sometimes written  (Koekoek and Swarttouw 1998, p. 7). -analogs provided the basis for the Askey-Wilson classification of all orthogonal polynomials.

A physical motivation for -special functions is provided by generalizing the canonical commutation relation

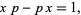(2)

where  is a generalized coordinate and 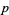 the corresponding generalized momentum, to

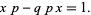(3)

For example, this immediately leads to the 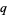-analog of the Hermite polynomial. 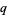-analogs preserve (or change only slightly) the form of the governing functional equations, and therefore arise in many physical applications, such as exact models in statistical mechanics, noncommutative geometry, and many-particle systems.

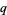-analogs also have a combinatorial interpretation based on the fact that one can count the elements of some set  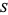to get the number 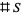. A so-called "statistic"  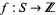can then be defined which is an integer-valued function on  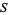and separates the elements of  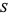into classes based on what value  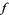takes on the elements. This relationship can be summarized by writing a polynomial in a new variable, usually taken as 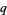, where the coefficient of  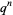is {s in S:f(s)=n}" src="http://mathworld.wolfram.com/images/equations/q-Analog/Inline30.gif" style="height:14px; width:108px" />. Evaluating the polynomial at 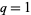then adds the coefficients together, returning the original .

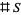The 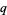-analog of a mathematical object is generally called the "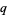-object," hence q-binomial coefficient, q-factorial, etc. There are generally several 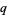-analogs if there is one, and there is sometimes even a multibasic analog with independent 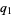, , 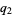.... Other types of analogs are also defined, for example the d-analog.

REFERENCES:

Andrews, G. E.; Askey, R.; and Roy, R. Special Functions. Cambridge, England: Cambridge University Press, 1999.

Exton, H. q-Hypergeometric Functions and Applications. New York: Halstead Press, 1983.

Koekoek, R. and Swarttouw, R. F. The Askey-Scheme of Hypergeometric Orthogonal Polynomials and its 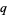-Analogue. Delft, Netherlands: Technische Universiteit Delft, Faculty of Technical Mathematics and Informatics Report 98-17, p. 7, 1998.

Koepf, W. Hypergeometric Summation: An Algorithmic Approach to Summation and Special Function Identities. Braunschweig, Germany: Vieweg, p. 26, 1998.

اخر الاخبار

اخبار العتبة العباسية المقدسة

قسم شؤون المعارف يطلق دورة (صفات الشيعة) لعدد من ملاكات العتبة العباسية المقدسة

الهيأة العليا لإحياء التراث تبحث تعزيز التعاون المشترك مع مركز الإمام الباقر (عليه السلام) في إيران

جامعة الكفيل تكرِّم طلبتها المتميزين من ذوي الاحتياجات الخاصة

فريق طبي في مستشفى الكفيل يجري عملية ناجحة لطفل يعاني من تشوّه ولاديّ بالنخاع الشوكي

المزيد

الآخبار الصحية

خصوصا مع تقدم السن.. 6 سلوكيات يومية قد تدمّر صحتك

فاكهة خضراء.. علاج طبيعي فعّال للإمساك واضطرابات الهضم

روسيا تبدأ أولى التجارب السريرية للقاح واعد ضد السرطان

كنز غذائي على طبقك.. ماذا تفعل السبانخ بجسمك؟

المزيد

الآخبار التكنلوجية

رصد نوع نادر من القطط في تايلاند للمرة الأولى منذ عقود

روسيا تخطط لإقامة محطة نووية في القمر خلال العقد المقبل

كيف قاد إيلون ماسك حملة "غروك" لاختراق عرش الذكاء الاصطناعي

ألتمان: الذكاء الاصطناعي سيتجاوز البشر في 2026 !

المزيد