


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 15-10-2019
Date: 25-5-2019
Date: 16-8-2018
|
There are several q-analogs of the cosine function.
The two natural definitions of the 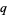 -cosine defined by Koekoek and Swarttouw (1998) are given by
-cosine defined by Koekoek and Swarttouw (1998) are given by
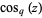 |
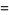 |
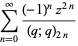 |
(1) |
 |
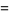 |
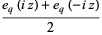 |
(2) |
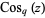 |
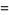 |
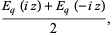 |
(3) |
where 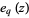 and
and 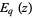 are q-exponential functions. The
are q-exponential functions. The 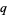 -cosine and
-cosine and 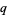 -sine functions satisfy the relations
-sine functions satisfy the relations
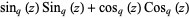 |
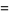 |
 |
(4) |
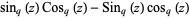 |
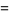 |
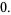 |
(5) |
Another definition of the 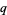 -cosine considered by Gosper (2001) is given by
-cosine considered by Gosper (2001) is given by
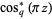 |
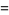 |
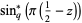 |
(6) |
 |
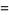 |
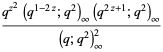 |
(7) |
 |
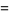 |
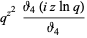 |
(8) |
 |
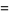 |
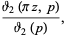 |
(9) |
where 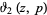 is a Jacobi theta function and
is a Jacobi theta function and 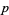 is defined via
is defined via
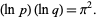 |
(10) |
This is an even function of unit amplitude, period 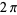 , and double and triple angle formulas and addition formulas which are analogous to ordinary sine and cosine. For example,
, and double and triple angle formulas and addition formulas which are analogous to ordinary sine and cosine. For example,
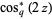 |
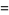 |
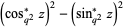 |
(11) |
 |
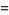 |
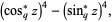 |
(12) |
where 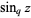 is the q-sine, and
is the q-sine, and 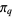 is q-pi (Gosper 2001). The
is q-pi (Gosper 2001). The 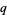 -cosine also satisfies
-cosine also satisfies
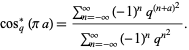 |
(13) |
REFERENCES:
Gosper, R. W. "Experiments and Discoveries in q-Trigonometry." In Symbolic Computation, Number Theory,Special Functions, Physics and Combinatorics. Proceedings of the Conference Held at the University of Florida, Gainesville, FL, November 11-13, 1999 (Ed. F. G. Garvan and M. E. H. Ismail). Dordrecht, Netherlands: Kluwer, pp. 79-105, 2001.
Koekoek, R. and Swarttouw, R. F. The Askey-Scheme of Hypergeometric Orthogonal Polynomials and its 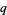 -Analogue. Delft, Netherlands: Technische Universiteit Delft, Faculty of Technical Mathematics and Informatics Report 98-17, pp. 18-19, 1998.
-Analogue. Delft, Netherlands: Technische Universiteit Delft, Faculty of Technical Mathematics and Informatics Report 98-17, pp. 18-19, 1998.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
دراسة تستعرض آلام السجناء السياسيين في حقبة البعث المجرم في العراق
|
|
|