
q-Hypergeometric Function
 المؤلف:
Andrews, G.
المؤلف:
Andrews, G.
 المصدر:
q-Series: Their Development and Application in Analysis, Number Theory, Combinatorics, Physics, and Computer Algebra. Providence, RI: Amer. Math
المصدر:
q-Series: Their Development and Application in Analysis, Number Theory, Combinatorics, Physics, and Computer Algebra. Providence, RI: Amer. Math
 الجزء والصفحة:
...
الجزء والصفحة:
...
 28-8-2019
28-8-2019
 2270
2270
q-Hypergeometric Function
The modern definition of the 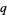 -hypergeometric function is
-hypergeometric function is
 |
(1)
|
where 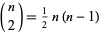 is a binomial coefficient and
is a binomial coefficient and 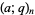 is a q-Pochhammer symbol (Gasper and Rahman 1990; Bhatnagar 1995, p. 21; Koepf 1998, p. 25). This is the version of the
is a q-Pochhammer symbol (Gasper and Rahman 1990; Bhatnagar 1995, p. 21; Koepf 1998, p. 25). This is the version of the 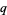 -hypergeometric function implemented in the Wolfram Language as QHypergeometricPFQ[
-hypergeometric function implemented in the Wolfram Language as QHypergeometricPFQ[![<span style=]() {" src="http://mathworld.wolfram.com/images/equations/q-HypergeometricFunction/Inline5.gif" style="height:14px; width:5px" />a1, ..., ar
{" src="http://mathworld.wolfram.com/images/equations/q-HypergeometricFunction/Inline5.gif" style="height:14px; width:5px" />a1, ..., ar![<span style=]() }" src="http://mathworld.wolfram.com/images/equations/q-HypergeometricFunction/Inline6.gif" style="height:14px; width:5px" />,
}" src="http://mathworld.wolfram.com/images/equations/q-HypergeometricFunction/Inline6.gif" style="height:14px; width:5px" />, ![<span style=]() {" src="http://mathworld.wolfram.com/images/equations/q-HypergeometricFunction/Inline7.gif" style="height:14px; width:5px" />b1, ..., bs
{" src="http://mathworld.wolfram.com/images/equations/q-HypergeometricFunction/Inline7.gif" style="height:14px; width:5px" />b1, ..., bs![<span style=]() }" src="http://mathworld.wolfram.com/images/equations/q-HypergeometricFunction/Inline8.gif" style="height:14px; width:5px" />, q, z].
}" src="http://mathworld.wolfram.com/images/equations/q-HypergeometricFunction/Inline8.gif" style="height:14px; width:5px" />, q, z].
An older form of definition omits the factor ![[(-1)^kq^((n; 2))]^(1+s-r)](http://mathworld.wolfram.com/images/equations/q-HypergeometricFunction/Inline9.gif) ,
,
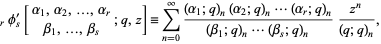 |
(2)
|
This is the 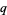 -hypergeometric function as defined by Bailey (1935), Slater (1966), Andrews (1986), and Hardy (1999).
-hypergeometric function as defined by Bailey (1935), Slater (1966), Andrews (1986), and Hardy (1999).
Note that the two definitions coincide when 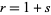 , including the common case
, including the common case 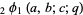 .
.
A particular case of 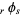 is given by
is given by
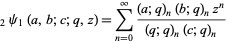 |
(3)
|
(Andrews 1986, p. 10). A 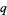 -analog of Gauss's theorem (the q-Gauss identity) due to Jacobi and Heine is given by
-analog of Gauss's theorem (the q-Gauss identity) due to Jacobi and Heine is given by
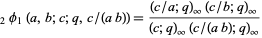 |
(4)
|
for 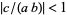 (Koepf 1998, p. 40). Heine proved the transformation formula
(Koepf 1998, p. 40). Heine proved the transformation formula
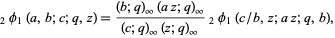 |
(5)
|
(Andrews 1986, pp. 10-11). Rogers (1893) obtained the formulas
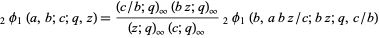 |
(6)
|
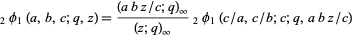 |
(7)
|
(Andrews 1986, pp. 10-11).
The function 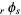 has the simple confluent identity
has the simple confluent identity
![lim_(alpha_r->infty)_rphi_s[alpha_1,alpha_2,...,alpha_r; beta_1,...,beta_s;q,z/(alpha_r)]=_(r-1)phi_s[alpha_1,alpha_2,...,alpha_(r-1); beta_1,...,beta_s;q,z].](http://mathworld.wolfram.com/images/equations/q-HypergeometricFunction/NumberedEquation8.gif) |
(8)
|
In the limit 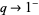 ,
,
![lim_(q->1^-)_rphi_s[q^(alpha_1),q^(alpha_2),...,q^(alpha_r); q^(beta_1),...,q^(beta_s);q,(q-1)^(1+s-r)z]=_rF_s[alpha_1,alpha_2,...,alpha_r; beta_1,...,beta_s;z],](http://mathworld.wolfram.com/images/equations/q-HypergeometricFunction/NumberedEquation9.gif) |
(9)
|
where 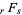 is a generalized hypergeometric function (Koepf 1998, p. 25).
is a generalized hypergeometric function (Koepf 1998, p. 25).
REFERENCES:
Andrews, G. E. q-Series: Their Development and Application in Analysis, Number Theory, Combinatorics, Physics, and Computer Algebra. Providence, RI: Amer. Math. Soc., p. 10, 1986.
Bailey, W. N. "Basic Hypergeometric Series." Ch. 8 in Generalised Hypergeometric Series. Cambridge, England: Cambridge University Press, pp. 65-72, 1935.
Bhatnagar, G. Inverse Relations, Generalized Bibasic Series, and their U(n) Extensions. Ph.D. thesis. Ohio State University, p. 21, 1995.
Gasper, G. and Rahman, M. Basic Hypergeometric Series. Cambridge, England: Cambridge University Press, 1990.
Gasper, G. "Elementary Derivations of Summation and Transformation Formulas for q-Series." In Fields Inst. Comm. 14 (Ed. M. E. H. Ismail et al. ), pp. 55-70, 1997.
Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, pp. 107-111, 1999.
Heine, E. "Über die Reihe 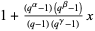
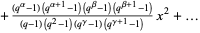 ." J. reine angew. Math. 32, 210-212, 1846.
." J. reine angew. Math. 32, 210-212, 1846.
Heine, E. "Untersuchungen über die Reihe 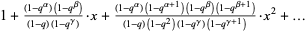 ." J. reine angew. Math. 34, 285-328, 1847.
." J. reine angew. Math. 34, 285-328, 1847.
Heine, E. Theorie der Kugelfunctionen und der verwandten Functionen, Bd. 1. Berlin: Reimer, pp. 97-125, 1878.
Koepf, W. Hypergeometric Summation: An Algorithmic Approach to Summation and Special Function Identities. Braunschweig, Germany: Vieweg, pp. 25-26, 1998.
Krattenthaler, C. "HYP and HYPQ." J. Symb. Comput. 20, 737-744, 1995.
Rogers, L. J. "On a Three-Fold Symmetry in the Elements of Heine's Series." Proc. London Math. Soc. 24, 171-179, 1893.
Slater, L. J. Generalized Hypergeometric Functions. Cambridge, England: Cambridge University Press, 1966.
 الاكثر قراءة في التفاضل و التكامل
الاكثر قراءة في التفاضل و التكامل
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


