
Ramanujan Theta Functions
 المؤلف:
Berndt, B. C.; Huang, S.-S.; Sohn, J.; and Son, S. H.
المؤلف:
Berndt, B. C.; Huang, S.-S.; Sohn, J.; and Son, S. H.
 المصدر:
"Some Theorems on the Rogers-Ramanujan Continued Fraction in Ramanujan,s Lost Notebook." Trans. Amer. Math. Soc. 352
المصدر:
"Some Theorems on the Rogers-Ramanujan Continued Fraction in Ramanujan,s Lost Notebook." Trans. Amer. Math. Soc. 352
 الجزء والصفحة:
...
الجزء والصفحة:
...
 31-8-2019
31-8-2019
 1905
1905
Ramanujan Theta Functions
Ramanujan's two-variable theta function 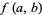 is defined by
is defined by
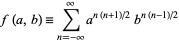 |
(1)
|
for 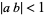 (Berndt 1985, p. 34; Berndt et al. 2000). It satisfies
(Berndt 1985, p. 34; Berndt et al. 2000). It satisfies
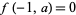 |
(2)
|
and
(Berndt 1985, pp. 34-35; Berndt et al. 2000), where 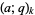 is a q-Pochhammer symbol, i.e., a q-series.
is a q-Pochhammer symbol, i.e., a q-series.
A one-argument form of 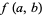 is also defined by
is also defined by
(OEIS A010815; Berndt 1985, pp. 36-37; Berndt et al. 2000), where 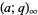 is a q-Pochhammer symbol. The identities above are equivalent to the pentagonal number theorem.
is a q-Pochhammer symbol. The identities above are equivalent to the pentagonal number theorem.
The function also satisfies
Ramanujan's 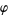 -function
-function 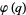 is defined by
is defined by
(OEIS A000122), where 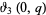 is a Jacobi theta function (Berndt 1985, pp. 36-37).
is a Jacobi theta function (Berndt 1985, pp. 36-37). 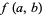 is a generalization of
is a generalization of 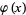 , with the two being connected by
, with the two being connected by
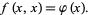 |
(15)
|
Special values of 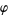 include
include
where 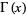 is a gamma function.
is a gamma function.
Ramanujan's 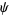 -function
-function 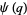 is defined by
is defined by
(OEIS A010054; Berndt 1985, p. 37).
Ramanujan's 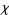 -function
-function 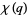 is defined by
is defined by
(OEIS A000700; Berndt 1985, p. 37).
A different 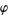 function is sometimes defined as
function is sometimes defined as
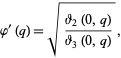 |
(27)
|
where 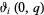 is again a Jacobi theta function, which has special value
is again a Jacobi theta function, which has special value
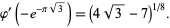 |
(28)
|
REFERENCES:
Berndt, B. C. Ramanujan's Notebooks, Part III. New York: Springer-Verlag, 1985.
Berndt, B. C.; Huang, S.-S.; Sohn, J.; and Son, S. H. "Some Theorems on the Rogers-Ramanujan Continued Fraction in Ramanujan's Lost Notebook." Trans. Amer. Math. Soc. 352, 2157-2177, 2000.
Mc Laughlin, J.; Sills, A. V.; and Zimmer, P. "Dynamic Survey DS15: Rogers-Ramanujan-Slater Type Identities." Electronic J. Combinatorics, DS15, 1-59, May 31, 2008. http://www.combinatorics.org/Surveys/ds15.pdf.
Sloane, N. J. A. Sequences A000122, A000700/M0217, A010054, and A010815 in "The On-Line Encyclopedia of Integer Sequences."
 الاكثر قراءة في التفاضل و التكامل
الاكثر قراءة في التفاضل و التكامل
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


