Rogers-Ramanujan Identities
For 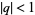 , the Rogers-Ramanujan identities are given by (Hardy 1999, pp. 13 and 90),
, the Rogers-Ramanujan identities are given by (Hardy 1999, pp. 13 and 90),
(OEIS A003114), and
(OEIS A003106), where 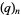 is a q-Pochhammer symbol.
is a q-Pochhammer symbol.
Polynomial generalizations of (◇) are given by
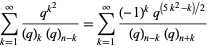 |
(5)
|
and
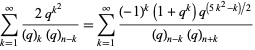 |
(6)
|
(Petkovšek et al. 1996). Even though they appear to be infinite series, only finitely many of the terms on each side are nonzero since 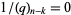 when
when 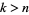 . (5) and (6) specify a sequence of polynomials, indexed by
. (5) and (6) specify a sequence of polynomials, indexed by 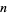 , as
, as 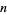 gets larger and larger, the polynomial approximates the series (◇) more and more closely. Also, taking the limit as
gets larger and larger, the polynomial approximates the series (◇) more and more closely. Also, taking the limit as 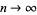 recovers (◇) after applying the Jacobi triple product identity on the right hand side. Finally, (5) and (6) are actually equivalent to each other; (6) is the "symmetrized" version of (5) using the so-called Paule symmetrization.
recovers (◇) after applying the Jacobi triple product identity on the right hand side. Finally, (5) and (6) are actually equivalent to each other; (6) is the "symmetrized" version of (5) using the so-called Paule symmetrization.
These identities can also be written even more succinctly as the single identity
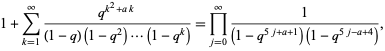 |
(7)
|
for 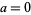 , 1.
, 1.
The formulas have a curious history, having been proved by Rogers (1894) in a paper that was completely ignored, then rediscovered (without proof) by Ramanujan sometime before 1913. The formulas were communicated to MacMahon, who published them in his famous text, still without proof. Then, in 1917, Ramanujan accidentally found Roger's 1894 paper while leafing through a journal. In the meantime, Schur (1917) independently rediscovered and published proofs for the identities (Hardy 1999, p. 91). Garsia and Milne (1981ab) gave the first proof of the Rogers-Ramanujan identities to construct a bijection between the relevant classes of partitions (Andrews 1986, p. 59).
Bailey (1947, 1949) systematically studied and generalized Rogers's work on Rogers-Ramanujan type identities.
Slater (1952) published a list of 130 identities of Rogers-Ramanujan type, some of which were already known, but many which were new and due to Slater. A few of these are summarized in the following table. Note that Slater's tabulation actually contained a number of identities listed twice, and a few listed three times, as a result of two different starting points sometimes leading to the same final result, but with a possibly with a slightly different algebraic presentation.
| identity number |
identity name |
| 42, 41, 40 |
Bailey Mod 9 identities |
| 93, 92, 91, 90 |
Dyson Mod 27 identities |
| 36, 34 |
Göllnitz-Gordon identities |
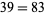 |
Jackson-Slater identity |
| 61, 60, 59 |
Rogers Mod 14 identities |
| 18, 14 |
Rogers-Ramanujan identities |
| 33, 32, 31 |
Rogers-Selberg identities |
Schur showed that (◇) has the combinatorial interpretation that the number of partitions of 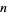 with minimal difference
with minimal difference 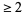 is equal to the number of partitions into parts of the forms
is equal to the number of partitions into parts of the forms 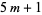 or
or 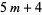 (Hardy 1999, p. 92). The following table gives the first few values.
(Hardy 1999, p. 92). The following table gives the first few values.
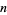 |
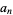 |
min. diff. |
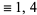 (mod 5) (mod 5) |
| 1 |
1 |
1 |
1 |
| 2 |
1 |
2 |
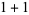 |
| 3 |
1 |
3 |
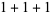 |
| 4 |
2 |
4, 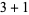 |
4, 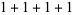 |
| 5 |
2 |
5, 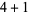 |
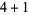 , , 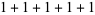 |
| 6 |
3 |
6, 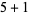 , , 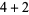 |
6, 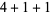 , , 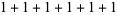 |
There is a similar combinatorial interpretation for (◇).
The Andrews-Gordon identity is generalization of the Rogers-Ramanujan identities.
There is a sequence of identities given by
1. The two Rogers-Ramanujan identities (triple product on mod 5 over 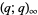 ).
).
2. The three Rogers-Selberg identities (triple product on mod 7 over 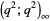 ).
).
3. The (sort of) four Bailey Mod 9 identities (triple product on mod 9 over 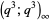 ).
).
4. The five identities due to Andrews (1975) of type (triple product on mod 11 over 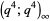 ), but the series representations are double series and therefore not as elegant as the other identities.
), but the series representations are double series and therefore not as elegant as the other identities.
5. The six double series expansions of type mod 13 over 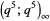 type products.
type products.
Here, "sort of" refers to the fact that between 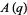 and
and 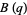 , there is an "identity" in which the product side contains
, there is an "identity" in which the product side contains 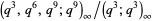 , so the identity reduces to
, so the identity reduces to 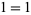 and therefore is not listed.
and therefore is not listed.
There is also a different sequence of identities given by
1. The Rogers-Ramanujan identities (2 identities mod 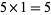 ).
).
2. The Rogers Mod 14 identities (3 identities mod 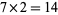 ).
).
3. The Dyson Mod 27 identities (4 identities mod 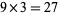 ).
).
The next in the sequence would be 5 identities with modulus 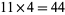 . A. Sills worked out a series expansion these identities, but it was so ugly that he did not publish it (A. Sills, pers. comm., Mar. 16, 2005).
. A. Sills worked out a series expansion these identities, but it was so ugly that he did not publish it (A. Sills, pers. comm., Mar. 16, 2005).
REFERENCES:
Andrews, G. E. "On Rogers-Ramanujan Type Identities Related to the Moduls 11." Proc. London Math. Soc. 30, 330-346, 1975.
Andrews, G. E. "The Hard-Hexagon Model and Rogers-Ramanujan Type Identities." Proc. Nat. Acad. Sci. U.S.A. 78, 5290-5292, 1981.
Andrews, G. E. Encyclopedia of Mathematics and Its Applications, Vol. 2: The Theory of Partitions. Cambridge, England: Cambridge University Press, pp. 109 and 238, 1984.
Andrews, G. E. q-Series: Their Development and Application in Analysis, Number Theory, Combinatorics, Physics, and Computer Algebra. Providence, RI: Amer. Math. Soc., pp. 17-20, 1986.
Andrews, G. E. and Baxter, R. J. "A Motivated Proof of the Rogers-Ramanujan Identities." Amer. Math. Monthly 96, 401-409, 1989.
Andrews, G. E. and Santos, J. P. O. "Rogers-Ramanujan Type Identities for Partitions with Attached Odd Parts." Ramanujan J. 1, 91-99, 1997.
Andrews, G. E.; Baxter, R. J.; and Forrester, P. J. "Eight-Vertex SOS Model and Generalized Rogers-Ramanujan-Type Identities." J. Stat. Phys. 35, 193-266, 1984.
Bailey, W. N. "Some Identities in Combinatory Analysis." Proc. London Math. Soc. 49, 421-435, 1947.
Bailey, W. N, "Identities of the Rogers-Ramanujan type." Proc. London Math. Soc., 50, 421-435, 1949.
Bressoud, D. M. Analytic and Combinatorial Generalizations of the Rogers-Ramanujan Identities. Providence, RI: Amer. Math. Soc., 1980.
Fulman, J. "The Rogers-Ramanujan Identities, The Finite General Linear Groups, and the Hall-Littlewood Polynomials." Proc. Amer. Math. Soc. 128, 17-25, 1999.
Garsia, A. M. and Milne, S. C. "A Method for Constructing Bijections for Classical Partition Identities." Proc. Nat. Acad. Sci. USA 78, 2026-2028, 1981a.
Garsia, A. M. and Milne, S. C. "A Rogers-Ramanujan Bijection." J. Combin. Th. Ser. A 31, 289-339, 1981b.
Guy, R. K. "The Strong Law of Small Numbers." Amer. Math. Monthly 95, 697-712, 1988.
Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, pp. 13 and 90-99, 1999.
Hardy, G. H. and Wright, E. M. "The Rogers-Ramanujan Identities." §19.13 in An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, pp. 290-294, 1979.
MacMahon, P. A. Combinatory Analysis, Vol. 2. New York: Chelsea, pp. 33-36, 1960.
Mc Laughlin, J.; Sills, A. V.; and Zimmer, P. "Dynamic Survey DS15: Rogers-Ramanujan-Slater Type Identities." Electronic J. Combinatorics, DS15, 1-59, May 31, 2008. http://www.combinatorics.org/Surveys/ds15.pdf.
Paule, P. "Short and Easy Computer Proofs of the Rogers-Ramanujan Identities and of Identities of Similar Type." Electronic J. Combinatorics 1, No. 1, R10, 1-9, 1994. http://www.combinatorics.org/Volume_1/Abstracts/v1i1r10.html.
Petkovšek, M.; Wilf, H. S.; and Zeilberger, D. A=B. Wellesley, MA: A K Peters, p. 117, 1996. http://www.cis.upenn.edu/~wilf/AeqB.html.
Ramanujan, S. Problem 584. J. Indian Math. Soc. 6, 199-200, 1914.
Robinson, R. M. "Comment to: 'A Motivated Proof of the Rogers-Ramanujan Identities.' " Amer. Math. Monthly 97, 214-215, 1990.
Rogers, L. J. "Second Memoir on the Expansion of Certain Infinite Products." Proc. London Math. Soc. 25, 318-343, 1894.
Rogers, L. J. "On Two Theorems of Combinatory Analysis and Some Allied Identities." Proc. London Math. Soc. 16, 315-336, 1917.
Rogers, L. J. "Proof of Certain Identities in Combinatory Analysis." Proc. Cambridge Philos. Soc. 19, 211-214, 1919.
Schur, I. "Ein Beitrag zur additiven Zahlentheorie und zur Theorie der Kettenbrüche." Sitzungsber. Preuss. Akad. Wiss. Phys.-Math. Klasse, pp. 302-321, 1917.
Slater, L. J. "Further Identities of the Rogers-Ramanujan Type." Proc. London Math. Soc. Ser. 2 54, 147-167, 1952.
Sloane, N. J. A. Sequences A003106/M0261, A003114/M0266, and A006141/M0260 in "The On-Line Encyclopedia of Integer Sequences."
Watson, G. N. "A New Proof of the Rogers-Ramanujan Identities." J. London Math. Soc. 4, 4-9, 1929.
Watson, G. N. "Theorems Stated by Ramanujan (VII): Theorems on Continued Fractions." J. London Math. Soc. 4, 39-48, 1929.
 الاكثر قراءة في التفاضل و التكامل
الاكثر قراءة في التفاضل و التكامل
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


