Riemann Zeta Function Zeros
Zeros of the Riemann zeta function 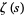 come in two different types. So-called "trivial zeros" occur at all negative even integers
come in two different types. So-called "trivial zeros" occur at all negative even integers 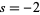 ,
, 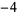 ,
, 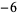 , ..., and "nontrivial zeros" occur at certain values of
, ..., and "nontrivial zeros" occur at certain values of 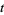 satisfying
satisfying
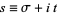 |
(1)
|
for 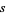 in the "critical strip"
in the "critical strip" 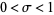 . In general, a nontrivial zero of
. In general, a nontrivial zero of 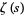 is denoted
is denoted 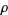 , and the
, and the 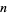 th nontrivial zero with
th nontrivial zero with 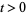 is commonly denoted
is commonly denoted 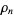 (Brent 1979; Edwards 2001, p. 43), with the corresponding value of
(Brent 1979; Edwards 2001, p. 43), with the corresponding value of 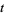 being called
being called 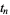 .
.
Wiener (1951) showed that the prime number theorem is literally equivalent to the assertion that 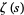 has no zeros on
has no zeros on 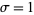 (Hardy 1999, p. 34; Havil 2003, p. 195). The Riemann hypothesis asserts that the nontrivial zeros of
(Hardy 1999, p. 34; Havil 2003, p. 195). The Riemann hypothesis asserts that the nontrivial zeros of 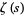 all have real part
all have real part ![sigma=R[s]=1/2](http://mathworld.wolfram.com/images/equations/RiemannZetaFunctionZeros/Inline18.gif) , a line called the "critical line." This is known to be true for the first
, a line called the "critical line." This is known to be true for the first 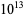 zeros.
zeros.

An attractive poster plotting zeros of the Riemann zeta function on the critical line together with annotations for relevant historical information, illustrated above, was created by Wolfram Research (1995).
The plots above show the real and imaginary parts of 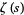 plotted in the complex plane together with the complex modulus of
plotted in the complex plane together with the complex modulus of 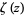 . As can be seen, in right half-plane, the function is fairly flat, but with a large number of horizontal ridges. It is precisely along these ridges that the nontrivial zeros of
. As can be seen, in right half-plane, the function is fairly flat, but with a large number of horizontal ridges. It is precisely along these ridges that the nontrivial zeros of 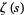 lie.
lie.
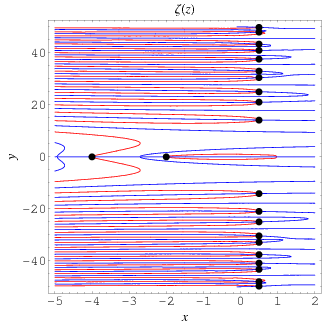
The position of the complex zeros can be seen slightly more easily by plotting the contours of zero real (red) and imaginary (blue) parts, as illustrated above. The zeros (indicated as black dots) occur where the curves intersect.
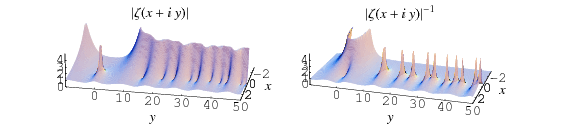
The figures above highlight the zeros in the complex plane by plotting 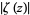 (where the zeros are dips) and
(where the zeros are dips) and 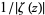 (where the zeros are peaks).
(where the zeros are peaks).
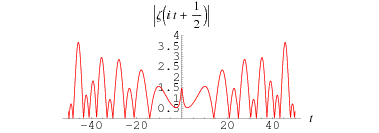
The above plot shows 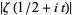 for
for 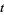 between 0 and 60. As can be seen, the first few nontrivial zeros occur at the values given in the following table (Wagon 1991, pp. 361-362 and 367-368; Havil 2003, p. 196; Odlyzko), where the corresponding negative values are also roots. The integers closest to these values are 14, 21, 25, 30, 33, 38, 41, 43, 48, 50, ... (OEIS A002410). The numbers of nontrivial zeros less than 10,
between 0 and 60. As can be seen, the first few nontrivial zeros occur at the values given in the following table (Wagon 1991, pp. 361-362 and 367-368; Havil 2003, p. 196; Odlyzko), where the corresponding negative values are also roots. The integers closest to these values are 14, 21, 25, 30, 33, 38, 41, 43, 48, 50, ... (OEIS A002410). The numbers of nontrivial zeros less than 10, 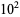 ,
, 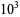 , ... are 0, 29, 649, 10142, 138069, 1747146, ... (OEIS A072080; Odlyzko).
, ... are 0, 29, 649, 10142, 138069, 1747146, ... (OEIS A072080; Odlyzko).
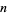 |
Sloane |
 |
| 1 |
A058303 |
14.134725 |
| 2 |
|
21.022040 |
| 3 |
|
25.010858 |
| 4 |
|
30.424876 |
| 5 |
|
32.935062 |
| 6 |
|
37.586178 |
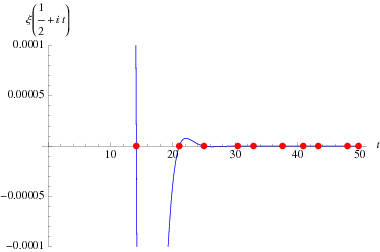
The so-called xi-function 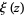 defined by Riemann has precisely the same zeros as the nontrivial zeros of
defined by Riemann has precisely the same zeros as the nontrivial zeros of 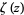 with the additional benefit that
with the additional benefit that 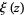 is entire and
is entire and 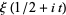 is purely real and so are simpler to locate.
is purely real and so are simpler to locate.
ZetaGrid is a distributed computing project attempting to calculate as many zeros as possible. It had reached 1029.9 billion zeros as of Feb. 18, 2005. Gourdon (2004) used an algorithm of Odlyzko and Schönhage to calculate the first 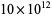 zeros (Pegg 2004, Pegg and Weisstein 2004). The following table lists historical benchmarks in the number of computed zeros (Gourdon 2004).
zeros (Pegg 2004, Pegg and Weisstein 2004). The following table lists historical benchmarks in the number of computed zeros (Gourdon 2004).
| year |
 |
author |
| 1903 |
15 |
J. P. Gram |
| 1914 |
79 |
R. J. Backlund |
| 1925 |
138 |
J. I. Hutchinson |
| 1935 |
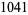 |
E. C. Titchmarsh |
| 1953 |
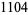 |
A. M. Turing |
| 1956 |
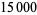 |
D. H. Lehmer |
| 1956 |
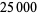 |
D. H. Lehmer |
| 1958 |
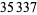 |
N. A. Meller |
| 1966 |
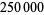 |
R. S. Lehman |
| 1968 |
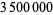 |
J. B. Rosser, J. M. Yohe, L. Schoenfeld |
| 1977 |
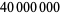 |
R. P. Brent |
| 1979 |
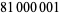 |
R. P. Brent |
| 1982 |
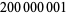 |
R. P. Brent, J. van de Lune, H. J. J. te Riele, D. T. Winter |
| 1983 |
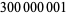 |
J. van de Lune, H. J. J. te Riele |
| 1986 |
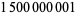 |
J. van de Lune, H. J. J. te Riele, D. T. Winter |
| 2001 |
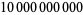 |
J. van de Lune (unpublished) |
| 2004 |
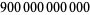 |
S. Wedeniwski |
| 2004 |
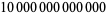 |
X. Gourdon and P. Demichel |
Numerical evidence suggests that all values of 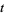 corresponding to nontrivial zeros are irrational (e.g., Havil 2003, p. 195; Derbyshire 2004, p. 384).
corresponding to nontrivial zeros are irrational (e.g., Havil 2003, p. 195; Derbyshire 2004, p. 384).
No known zeros with order greater than one are known. While the existence of such zeros would not disprove the Riemann hypothesis, it would cause serious problems for many current computational techniques (Derbyshire 2004, p. 385).
Some nontrivial zeros lie extremely close together, a property known as Lehmer's phenomenon.
The Riemann zeta function can be factored over its nontrivial zeros 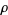 as the Hadamard product
as the Hadamard product
![zeta(s)=(e^([ln(2pi)-1-gamma/2]s))/(2(s-1)Gamma(1+1/2s))product_(rho)(1-s/rho)e^(s/rho)](http://mathworld.wolfram.com/images/equations/RiemannZetaFunctionZeros/NumberedEquation2.gif) |
(2)
|
(Titchmarsh 1987, Voros 1987).
Let 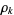 denote the
denote the 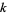 th nontrivial zero of
th nontrivial zero of 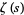 , and write the sums of the negative integer powers of such zeros as
, and write the sums of the negative integer powers of such zeros as
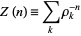 |
(3)
|
(Lehmer 1988, Keiper 1992, Finch 2003, p. 168), sometimes also denoted 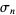 (e.g., Finch 2003, p. 168). But by the functional equation, the nontrivial zeros are paired as
(e.g., Finch 2003, p. 168). But by the functional equation, the nontrivial zeros are paired as 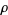 and
and 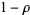 , so if the zeros with positive imaginary part are written as
, so if the zeros with positive imaginary part are written as 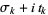 , then the sums become
, then the sums become
![Z(n)=sum_(k)[(sigma_k+it_k)^(-n)+(1-sigma_k-it_k)^(-n)].](http://mathworld.wolfram.com/images/equations/RiemannZetaFunctionZeros/NumberedEquation4.gif) |
(4)
|
Such sums can be computed analytically, and the first few are
where 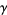 is the Euler-Mascheroni constant,
is the Euler-Mascheroni constant, 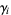 are Stieltjes constants,
are Stieltjes constants, 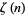 is the Riemann zeta function, and
is the Riemann zeta function, and 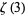 is Apéry's constant. These values can also be written in terms of the Li constants (Bombieri and Lagarias 1999).
is Apéry's constant. These values can also be written in terms of the Li constants (Bombieri and Lagarias 1999).
The case
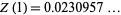 |
(11)
|
(OEIS A074760; Edwards 2001, p. 160) is classical and was known to Riemann, who used it in his computation of the roots of 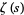 (Davenport 1980, pp. 83-84; Edwards 2001, pp. 67 and 159). It is also equal to the constant
(Davenport 1980, pp. 83-84; Edwards 2001, pp. 67 and 159). It is also equal to the constant 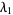 from Li's criterion.
from Li's criterion.
Assuming the truth of the Riemann hypothesis (so that 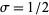 ), equation (◇) can be written for the first few values of
), equation (◇) can be written for the first few values of 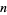 in the simple forms
in the simple forms
and so on.
REFERENCES:
Bombieri, E. and Lagarias, J. C. "Complements to Li's Criterion for the Riemann Hypothesis." J. Number Th. 77, 274-287, 1999.
Brent, R. P. "On the Zeros of the Riemann Zeta Function in the Critical Strip." Math. Comput. 33, 1361-1372, 1979.
Brent, R. P.; van de Lune, J.; te Riele, H. J. J.; and Winter, D. T. "On the Zeros of the Riemann Zeta Function in the Critical Strip. II." Math. Comput. 39, 681-688, 1982.
Davenport, H. Multiplicative Number Theory, 2nd ed. New York: Springer-Verlag, 1980.
Derbyshire, J. Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics. New York: Penguin, 2004.
Edwards, H. M. Riemann's Zeta Function. New York: Dover, 2001.
Farmer, D. W. "Counting Distinct Zeros of the Riemann Zeta-Function." Electronic J. Combinatorics 2, No. 1, R1, 1-5, 1995. http://www.combinatorics.org/Volume_2/Abstracts/v2i1r1.html.
Finch, S. R. Mathematical Constants. Cambridge, England: Cambridge University Press, p. 168, 2003.
Gourdon, X. "Computation of Zeros of the Zeta Function." http://numbers.computation.free.fr/Constants/Miscellaneous/zetazeroscompute.html.
Gourdon, X. "The 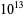 First Zeros of the Riemann Zeta Function, and Zeros Computation at Very Large Height." Oct. 24, 2004. http://numbers.computation.free.fr/Constants/Miscellaneous/zetazeros1e13-1e24.pdf.
First Zeros of the Riemann Zeta Function, and Zeros Computation at Very Large Height." Oct. 24, 2004. http://numbers.computation.free.fr/Constants/Miscellaneous/zetazeros1e13-1e24.pdf.
Gram, J.-P. "Sur les zéros de la fonction 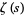 de Riemann." Acta Math. 27, 289-304, 1903.
de Riemann." Acta Math. 27, 289-304, 1903.
Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, 1999.
Havil, J. "The Zeros of Zeta." §16.6 in Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, pp. 193-196, 2003.
Hayes, B. "The Spectrum of Riemannium." Amer. Sci. 91, 296-300, 2003.
Hutchinson, J. I. "On the Roots of the Riemann Zeta-Function." Trans. Amer. Math. Soc. 27, 49-60, 1925.
Keiper, J. B. "Power Series Expansions of Riemann's 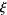 Function." Math. Comput. 58, 765-773, 1992.
Function." Math. Comput. 58, 765-773, 1992.
Landau, E. "Über die Nullstellen der Zetafunction." Math. Ann. 71, 548-564, 1911.
Lehmer, D. H. "The Sum of Like Powers of the Zeros of the Riemann Zeta Function." Math. Comput. 50, 265-273, 1988.
Odlyzko, A. M. "The 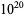 th Zero of the Riemann Zeta Function and 70 Million of Its Neighbors." Preprint.
th Zero of the Riemann Zeta Function and 70 Million of Its Neighbors." Preprint.
Odlyzko, A. "Tables of Zeros of the Riemann Zeta Function." http://www.dtc.umn.edu/~odlyzko/zeta_tables/.
Pegg, E. Jr. "Math Games: Ten Trillion Zeta Zeros." Oct. 18, 2004. http://www.maa.org/editorial/mathgames/mathgames_10_18_04.html.
Pegg, E. Jr. and Weisstein, E. W. "Seven Mathematical Tidbits." MathWorld Headline News. Nov. 8, 2004. http://mathworld.wolfram.com/news/2004-11-08/seventidbits/#3.
Sabbagh, K. Dr. Riemann's Zeros: The Search for the $1 Million Solution to the Greatest Problem in Mathematics. Atlantic Books, 2002.
Sloane, N. J. A. Sequences A002410/M4924, A058303, A072080, and A074760 in "The On-Line Encyclopedia of Integer Sequences."
Titchmarsh, E. C. The Theory of the Riemann Zeta Function, 2nd ed. New York: Clarendon Press, 1987.
Voros, A. "Spectral Functions, Special Functions and the Selberg Zeta Function." Commun. Math. Phys. 110, 439-465, 1987.
Wagon, S. "The Evidence: Where Are the Zeros of Zeta of 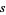 ?" Math. Intel. 8, 57-62, 1986.
?" Math. Intel. 8, 57-62, 1986.
Wagon, S. Mathematica in Action. New York: W. H. Freeman, 1991.
Wiener, N. §19 et seq. in The Fourier Integral and Certain of Its Applications. New York: Dover, 1951.
Wolfram Research. "The Riemann Zeta Function on the Critical Line Plotted by Mathematica." 1995. http://mathworld.wolfram.com/pdf/posters/Zeta.pdf.
ZetaGrid. http://www.zetagrid.net/.
 الاكثر قراءة في التفاضل و التكامل
الاكثر قراءة في التفاضل و التكامل
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


