Let 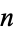 be an integer such that 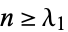, where  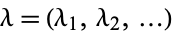is a partition o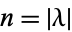f  if 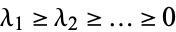, where  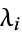are a sequence of positive integers stabilizing 0 such that 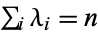. Also let  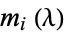be the number of parts of  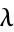of size 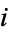. Then the permutation 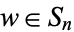, where  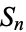is the symmetric group, acts on the variables 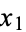, ...,  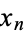by sending  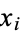to 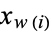. Letting  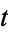be a complex number, the Hall-Littlewood polynomials are defined by

These polynomials interpolate between the Schur functions (with 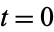) and the monomial symmetric functions (with 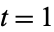; Fulman 1999).

REFERENCES:

Fulman, J. "The Rogers-Ramanujan Identities, the Finite General Linear Groups, and the Hall-Littlewood Polynomials." Proc. Amer. Math. Soc. 128, 17-25, 1999.

Macdonald, I. G. Symmetric Functions and Hall Polynomials, 2nd ed. Oxford, England: Oxford University Press, p. 208, 1995.

اخر الاخبار

اخبار العتبة العباسية المقدسة

قسم الإعلام يشارك في الاجتماع التحضيري لمناقشة الخطة الإعلامية لزيارة عاشوراء

بحضور متوليها الشرعي.. العتبة العباسية المقدسة تواصل إقامة المجالس الحسينية لإحياء شهر المحرم

قسم الشؤون الفكرية يطلق برنامجه التبليغي في أكثر من 20 دولة إفريقية

شعبتا الخطابة النسوية والتوجيه الديني تواصلان إقامة المجالس الحسينية في مرقد أبي الفضل العباس (عليه السلام)

المزيد

الآخبار الصحية

دراسة تكشف علاقة خطيرة بين عمر الأم وصحة مولودها

دراسة تحذر.. اضطراب نوم بسيط قد يسبب الموت المبكر ؟

الاستحمام بالماء الساخن.. راحة مؤقتة وأضرار دائمة للبشرة

ماذا يحدث للجسم عند تخطي وجبة الإفطار؟

المزيد

الآخبار التكنلوجية

كيف تساعد الصيانة الوقائية في الحفاظ على كفاءة التكييف في سيارتك ؟

في ظاهرة غريبة حيرت العلماء.. كوكبنا قد يسجل أقصر يوم في التاريخ هذا الصيف!

السد الصيني العملاق يعيق دوران الأرض ويغيّر شكلها ؟

السعودية تطلق 10 تجارب علمية إلى محطة الفضاء الدولية

المزيد