
Rectangle Function
 المؤلف:
Bracewell, R.
المؤلف:
Bracewell, R.
 المصدر:
"Rectangle Function of Unit Height and Base, Pi(x)." In The Fourier Transform and Its Applications. New York: McGraw-Hill,
المصدر:
"Rectangle Function of Unit Height and Base, Pi(x)." In The Fourier Transform and Its Applications. New York: McGraw-Hill,
 الجزء والصفحة:
pp. 52-53
الجزء والصفحة:
pp. 52-53
 29-9-2019
29-9-2019
 2689
2689
Rectangle Function
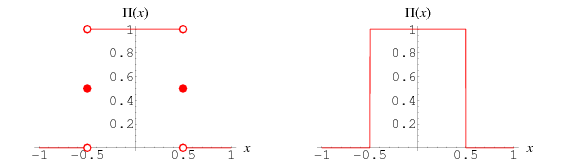
The rectangle function 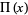 is a function that is 0 outside the interval
is a function that is 0 outside the interval ![[-1/2,1/2]](http://mathworld.wolfram.com/images/equations/RectangleFunction/Inline2.gif) and unity inside it. It is also called the gate function, pulse function, or window function, and is defined by
and unity inside it. It is also called the gate function, pulse function, or window function, and is defined by
![Pi(x)=<span style=]() {0 for |x|>1/2; 1/2 for |x|=1/2; 1 for |x|<1/2. " src="http://mathworld.wolfram.com/images/equations/RectangleFunction/NumberedEquation1.gif" style="height:86px; width:142px" /> {0 for |x|>1/2; 1/2 for |x|=1/2; 1 for |x|<1/2. " src="http://mathworld.wolfram.com/images/equations/RectangleFunction/NumberedEquation1.gif" style="height:86px; width:142px" /> |
(1)
|
The left figure above plots the function as defined, while the right figure shows how it would appear if traced on an oscilloscope. The generalized function 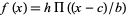 has height
has height 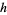 , center
, center 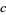 , and full-width
, and full-width 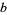 .
.
As noted by Bracewell (1965, p. 53), "It is almost never important to specify the values at 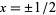 , that is at the points of discontinuity. Likewise, it is not necessary or desirable to emphasize the values
, that is at the points of discontinuity. Likewise, it is not necessary or desirable to emphasize the values 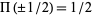 in graphs; it is preferable to show graphs which are reminiscent of high-quality oscillograms (which, of course, would never show extra brightening halfway up the discontinuity)."
in graphs; it is preferable to show graphs which are reminiscent of high-quality oscillograms (which, of course, would never show extra brightening halfway up the discontinuity)."
The piecewise version of the rectangle function is implemented in the Wolfram Language as UnitBox[x], while the generalized function version is implemented as HeavisidePi[x].
Identities satisfied by the rectangle function include
where 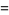 is the Heaviside step function. The Fourier transform of the rectangle function is given by
is the Heaviside step function. The Fourier transform of the rectangle function is given by
where 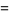 is the sinc function.
is the sinc function.
REFERENCES:
Bracewell, R. "Rectangle Function of Unit Height and Base, 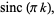 ." In The Fourier Transform and Its Applications. New York: McGraw-Hill, pp. 52-53, 1965.
." In The Fourier Transform and Its Applications. New York: McGraw-Hill, pp. 52-53, 1965.
 الاكثر قراءة في التفاضل و التكامل
الاكثر قراءة في التفاضل و التكامل
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


