
Lehmer Cotangent Expansion
 المؤلف:
Lehmer, D. H
المؤلف:
Lehmer, D. H
 المصدر:
"A Cotangent Analogue of Continued Fractions." Duke Math. J. 4
المصدر:
"A Cotangent Analogue of Continued Fractions." Duke Math. J. 4
 الجزء والصفحة:
...
الجزء والصفحة:
...
 13-10-2019
13-10-2019
 1454
1454
Lehmer Cotangent Expansion
Lehmer (1938) showed that every positive irrational number  has a unique infinite continued cotangent representation of the form
has a unique infinite continued cotangent representation of the form
![x=cot[sum_(k=0)^infty(-1)^kcot^(-1)b_k],](http://mathworld.wolfram.com/images/equations/LehmerCotangentExpansion/NumberedEquation1.gif) |
(1)
|
where the 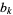 s are nonnegative and
s are nonnegative and
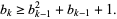 |
(2)
|
Note that this growth condition on coefficients is essential for the uniqueness of Lehmer expansion.
The following table summarizes the coefficients 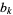 for various special constants.
for various special constants.
 |
OEIS |
![<span style=]() {b_k}" src="http://mathworld.wolfram.com/images/equations/LehmerCotangentExpansion/Inline5.gif" style="height:15px; width:23px" /> {b_k}" src="http://mathworld.wolfram.com/images/equations/LehmerCotangentExpansion/Inline5.gif" style="height:15px; width:23px" /> |
| e |
A002668 |
2, 8, 75, 8949, 119646723, 15849841722437093, ... |
Euler-Mascheroni constant 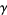 |
A081782 |
0, 1, 3, 16, 389, 479403, 590817544217, ... |
golden ratio 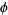 |
A006267 |
1, 4, 76, 439204, 84722519070079276, ... |
Lehmer's constant 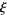 |
A002065 |
0, 1, 3, 13, 183, 33673, ... |
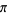 |
A002667 |
3, 73, 8599, 400091364,371853741549033970, ... |
Pythagoras's constant 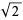 |
A002666 |
1, 5, 36, 3406, 14694817,727050997716715, ... |
The expansion for the golden ratio 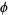 has the beautiful closed form
has the beautiful closed form
![phi=cot[sum_(k=0)^infty(-1)^kcot^(-1)(L_(3^k))],](http://mathworld.wolfram.com/images/equations/LehmerCotangentExpansion/NumberedEquation3.gif) |
(3)
|
where 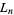 is a Lucas number.
is a Lucas number.
An illustration of a different cotangent expansion for 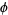 that is not a Lehmer expansion because its coefficients grow too slowly is
that is not a Lehmer expansion because its coefficients grow too slowly is
![phi=cot[sum_(k=0)^infty(-1)^kcot^(-1)(F_(2k+2))],](http://mathworld.wolfram.com/images/equations/LehmerCotangentExpansion/NumberedEquation4.gif) |
(4)
|
where 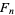 is a Fibonacci number (B. Cloitre, pers. comm., Sep. 22, 2005).
is a Fibonacci number (B. Cloitre, pers. comm., Sep. 22, 2005).
REFERENCES:
Lehmer, D. H. "A Cotangent Analogue of Continued Fractions." Duke Math. J. 4, 323-340, 1938.
Rivoal, T. "Propriétés diophantiennes du développement en cotangente continue de Lehmer." http://www-fourier.ujf-grenoble.fr/~rivoal/articles/cotan.pdf.
Shallit, J. "Predictable Regular Continued Cotangent Expansions." J. Res. Nat. Bur. Standards Sect. B 80B, 285-290, 1976.
Sloane, N. J. A. Sequences A002065/M2961, A002666/M3983, A002668/M1900, A002667/M3171, A006267/M3699, and A081782 in "The On-Line Encyclopedia of Integer Sequences."
 الاكثر قراءة في التفاضل و التكامل
الاكثر قراءة في التفاضل و التكامل
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


