


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 3-6-2019
Date: 28-7-2019
Date: 12-8-2018
|
The functions (also called the circular functions) comprising trigonometry: the cosecant 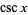 , cosine
, cosine 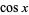 , cotangent
, cotangent 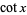 , secant
, secant 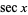 , sine
, sine 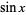 , and tangent
, and tangent 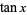 . However, other notations are sometimes used, as summarized in the following table.
. However, other notations are sometimes used, as summarized in the following table.
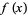 |
alternate notations |
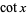 |
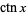 (Erdélyi et al. 1981, p. 7), (Erdélyi et al. 1981, p. 7), 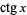 (Gradshteyn and Ryzhik 2000, p. xxix) (Gradshteyn and Ryzhik 2000, p. xxix) |
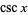 |
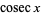 (Gradshteyn and Ryzhik 2000, p. xxvii) (Gradshteyn and Ryzhik 2000, p. xxvii) |
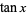 |
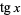 (Gradshteyn and Ryzhik 2000, p. xxix) (Gradshteyn and Ryzhik 2000, p. xxix) |
The inverses of these functions (the inverse trigonometric functions) are denoted 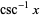 ,
, 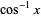 ,
, 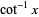 ,
, 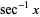 ,
, 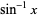 , and
, and 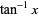 . Note that the
. Note that the 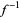 notation here means inverse function, not
notation here means inverse function, not 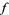 to the
to the 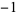 power.
power.
REFERENCES:
Erdélyi, A.; Magnus, W.; Oberhettinger, F.; and Tricomi, F. G. Higher Transcendental Functions, Vol. 1. New York: Krieger, p. 6, 1981.
Feynman, R. P. "A Different Set of Tools." In 'Surely You're Joking, Mr. Feynman!': Adventures of a Curious Character. New York: W. W. Norton, 1997.
Gradshteyn, I. S. and Ryzhik, I. M. Tables of Integrals, Series, and Products, 6th ed. San Diego, CA: Academic Press, 2000.



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
شعبة فاطمة بنت أسد (عليها السلام) تنظم دورة تخصصية في أحكام التلاوة
|
|
|