


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 24-7-2020
Date: 20-12-2020
Date: 20-8-2020
|

A golden rhombohedron is a rhombohedron whose faces consist of congruent golden rhombi. Golden rhombohedra are therefore special cases of a trigonal trapezohedron as well as zonohedra.
There are two distinct golden rhombohedra: the acute golden rhombohedron and obtuse golden rhombohedron. Both are built from six golden rhombi and comprise two of the five golden isozonohedra. These polyhedra are implemented in the Wolfram Language as PolyhedronData["AcuteGoldenRhombohedron"] and PolyhedronData["ObtuseGoldenRhombohedron"], respectively.
The acute and obtuse golden rhombohedra with edge length 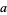 both have surface area
both have surface area
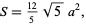 |
(1) |
and have volumes
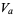 |
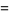 |
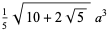 |
(2) |
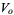 |
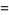 |
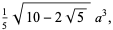 |
(3) |
respectively.
REFERENCES:
Kabai, S. Mathematical Graphics I: Lessons in Computer Graphics Using Mathematica. Püspökladány, Hungary: Uniconstant, pp. 169 and 171, 2002.
Livio, M. The Golden Ratio: The Story of Phi, the World's Most Astonishing Number. New York: Broadway Books, p. 206, 2002.



|
|
|
|
دراسة: حفنة من الجوز يوميا تحميك من سرطان القولون
|
|
|
|
|
|
|
تنشيط أول مفاعل ملح منصهر يستعمل الثوريوم في العالم.. سباق "الأرنب والسلحفاة"
|
|
|
|
|
|
|
لتعزيز التواصل مع الزائرات الأجنبيات : العتبة العلويّة المقدّسة تُطلق دورة لتعليم اللغة الإنجليزية لخادمات القسم النسويّ
|
|
|