


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 24-11-2020
Date: 16-8-2020
Date: 25-11-2020
|
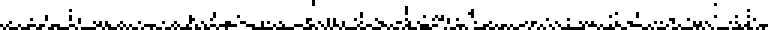
The continued fraction for 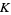 is [2; 1, 2, 5, 1, 1, 2, 1, 1, ...] (OEIS A002211). A plot of the first 256 terms of the continued fraction represented as a sequence of binary bits is shown above.
is [2; 1, 2, 5, 1, 1, 2, 1, 1, ...] (OEIS A002211). A plot of the first 256 terms of the continued fraction represented as a sequence of binary bits is shown above.
The convergents are 2, 3, 8/3, 43/16, 51/19, ... (OEIS A127005 and A127006).
The incrementally largest terms are 2, 5, 10, 24, 90, 770, ... (OEIS A054866), which occur at positions 0, 3, 10, 15, 23, 104, 1701, ... (OEIS A224852; illustrated above).
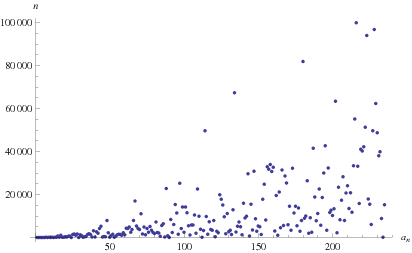
The plot above shows the positions of the first occurrences of 1, 2, 3, ... in the continued fraction, the first few of which are 1, 0, 9, 46, 3, 33, 75, 64, 118, 10, 103, 26, 102, 109, ... (OEIS A224851). The smallest number not occurring in the first 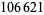 terms of the continued fraction are 236, 260, 265, 279, 282, ... (E. Weisstein, Jul. 22, 2013).
terms of the continued fraction are 236, 260, 265, 279, 282, ... (E. Weisstein, Jul. 22, 2013).
REFERENCES:
Havermann, H. "Simple Continued Fraction Expansion of Khinchin's Constant." http://odo.ca/~haha/cfk.html.
Sloane, N. J. A. Sequences A002211/M1564, A054866, A127005, A127006, A224851, and A224852 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|