Measuring distance in the Solar System: The Moon

The Moon is the only natural object in the Solar System whose distance can be found accurately using the classical parallax method.
In principle, it involves the simultaneous measurement of the meridian zenith distance of the Moon at two observatories with the same longitude but widely separated in latitude. The wide latitude separation provides a reasonably long base-line Let observatories O₁ and O₂ have latitudes ∅₁ N and ∅₂ S. Let the meridian zenith distances of the Moon be z₁₀ and z₂₀ at these two observatories, that is Z₁₀ = ∠Z₁O₁M and Z₂₀ = ∠Z₂O₂M (see figure 1).
Then if z₁ and z₂ are the true (i.e. geocentric) zenith distances for observatories O₁ and O₂ respectively, with p₁ and p₂ the parallactic angles O₁MC and O₂MC, we may write
∅₁ + ∅₂ = z₁ + z2 (1)
z₁ = z₁₀ − p₁ z₂ = z₂₀ − p₂ (2)
p₁ = P sin z₁₀ p₂ = P sin z₂₀ (3)
where P is the value of the Moon’s horizontal parallax when the observations are made.
By equations (3),
P = (p₁ + p₂)/(sin z₁₀ + sin z₂₀).
By equations (2),
p₁ + p₂ = z₁₀ + z₂₀ − (z₁ + z₂).
By equation (1), then, we have
P = [z₁₀ + z₂₀ − (∅₁ + ∅₂)]/(sin z₁₀ + sin z₂₀) (4)

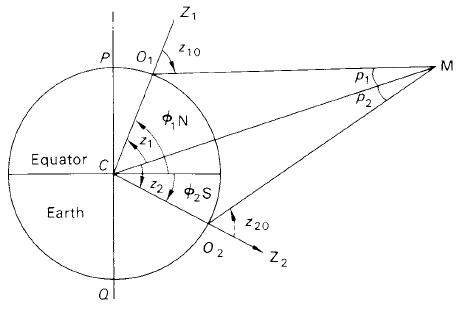
Figure 1. Measurement of the Moon’s distance by observations from two sites.
so that P may be calculated from known and measured quantities. Knowing the radius of the Earth.
In practice, the procedure is complicated by a number of factors. The observatories are never quite on the same meridian of longitude so that a correction has to be made for the change in the Moon’s declination in the time interval between its transits across the two observatories’ respective meridians. In addition, theMoon is not a point source of light. Agreement, therefore, has to be made between the observatories as to which crater to observe, a correction thereafter giving the distance between the centres of Earth and Moon.
Due allowance must be made for the individual instrumental errors and the local values of refraction. In the case of the Moon, its parallax is so large that any residual error is not great. Since the advent of radar, laser methods and lunar probes, including lunar artificial satellites, the Moon’s distance can be measured very accurately. The limiting accuracy is partly due to the accuracy with which the velocity of light is known but also involves the accuracy with which the Earth observing stations’ geodetic positions are known. Uncertainties are of the order of 0·1 of a metre, the average
distance being 384 400 kilometres. 

اخر الاخبار

اخبار العتبة العباسية المقدسة

عباس.. طفل فقد والده فوجد في خدمة زائري عاشوراء وطنًا آمنًا

شعبة الخطابة النسوية تواصل إقامة مجالس العزاء في شهر المحرم الحرام

لليوم الخامس.. العتبة العباسية المقدسة تقيم مجلس عزاء في صحن مرقد أبي الفضل العباس (عليه السلام)

قسم الشؤون الفكرية يقيم مجلس عزاء حسيني في العاصمة التنزانية دار السلام

المزيد

الآخبار الصحية

لمن تجاوز الستين.. عليك بشرب 4 أكواب من القهوة يوميا ؟

الحليب مع العسل.. مزيج يمنحك 7 فوائد صحية

لا تبالغ في التنظيف.. قليل من "الاتساخ" قد يحمي عائلتك

دراسة تكشف علاقة خطيرة بين عمر الأم وصحة مولودها

المزيد

الآخبار التكنلوجية

هل هاتفك مراقب؟.. 5 علامات خطيرة تكشف التجسس عليك

دبي تطلق أول رحلة تجريبية للتاكسي الجوي

كيف تساعد الصيانة الوقائية في الحفاظ على كفاءة التكييف في سيارتك ؟

في ظاهرة غريبة حيرت العلماء.. كوكبنا قد يسجل أقصر يوم في التاريخ هذا الصيف!

المزيد

مواضيع ذات صلة

اختبار الانفجار الهائل

الكوسمولوجيا وأشكال كالابي - ياو

التخمينات الكوسمولوجيا والنظرية النهائية

النموذج القياسي للكوسمولوجيا، أو علم الكون

تأملات في علم الكون

المذنبات

الصعود إلى الفضاء

اختلاف الليل والنهار

تصنيع الصاروخ و اطلاقة

الكويكبات والمذنبات

صورة الحجر الأزتكي (فهم وإدراك الحضارة الآزيتية )

الهالات المجرية