
Effect of precession on a star’s equatorial coordinates
 المؤلف:
A. Roy, D. Clarke
المؤلف:
A. Roy, D. Clarke
 المصدر:
Astronomy - Principles and Practice 4th ed
المصدر:
Astronomy - Principles and Practice 4th ed
 الجزء والصفحة:
p 144
الجزء والصفحة:
p 144
 5-8-2020
5-8-2020
 2289
2289
Effect of precession on a star’s equatorial coordinates
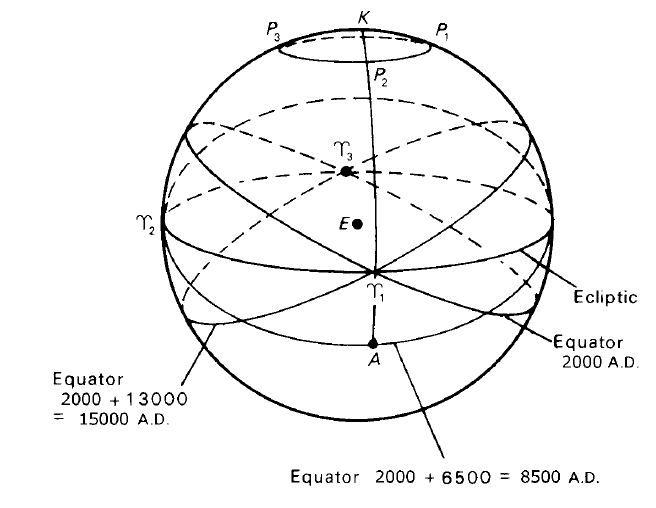
Figure 1. The celestial sphere illustrating the precessional movement of the celestial equator.
Let us consider now the sort of changes made in the star’s coordinates by precession, taking the precessional period to be 26 000 years. In figure 1, the north pole K of the ecliptic is set at the top of the diagram, with the ecliptic as shown. This is often a convenient orientation for a diagram in problems on precession where the north celestial pole and the celestial equator shift.
Let P1, P2, P3, be the positions of the north celestial pole now (2000 AD say), one-quarter and one-half of the precessional period later. The corresponding positions of  are
are 1,
1,  2,
2, 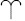 3. The various celestial equators are also inserted.
3. The various celestial equators are also inserted.
Consider a star whose present right ascension and declination are 0h and 0◦ respectively. The star is, therefore, at 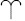 1 on the celestial sphere.
1 on the celestial sphere.
By 8500 AD, the First Point of Aries and the north celestial pole have moved to positions 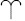 2 and P2 because of precession, and the meridian from the north celestial pole of that date through the star will cut the equator of that date at A. The star’s equatorial coordinates are then RA = 6h, Dec = ε◦ N, since
2 and P2 because of precession, and the meridian from the north celestial pole of that date through the star will cut the equator of that date at A. The star’s equatorial coordinates are then RA = 6h, Dec = ε◦ N, since 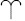 2A is of length 90◦. That this is so is seen from the fact that
2A is of length 90◦. That this is so is seen from the fact that 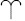 2 is the pole of the great circle K P2
2 is the pole of the great circle K P2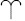 1.
1.
By 15 000 AD, the positions of the north celestial pole and First Point of Aries are P3 and 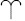 3. The coordinates of the star are now 12h, 0◦. Obviously, after three-quarters of the precessional period has passed, the star’s coordinates will be 18h, ε◦ S, its coordinates returning to their 2000 AD values after one complete precessional period has elapsed.
3. The coordinates of the star are now 12h, 0◦. Obviously, after three-quarters of the precessional period has passed, the star’s coordinates will be 18h, ε◦ S, its coordinates returning to their 2000 AD values after one complete precessional period has elapsed.
The present pole star, Polaris, is about one degree from the north celestial pole and so is a fair indicator of the pole’s position at the present day. If a star-map is obtained and a circle of radius ε (∼231/2◦) is traced about the north pole of the ecliptic, this circle will pass through the positions that have been or will be occupied by the north celestial pole. For example, some 4000 years ago, the bright star γ Draconis was about 4◦ from the pole; and in 12 000 years time, the pole will be within a few degrees of the bright star α Lyrae (Vega).
Star catalogues give the coordinates of stars with respect to a particular equator and vernal equinox, i.e. the positions the equator and equinox occupied at a particular epoch, say, the beginning of the years 1950, 1975 or 2000. The stellar positions in The Astronomical Almanac and other almanacs are also with reference to the position of the equator and equinox of a certain date—in this case the beginning of the year for which the almanac has been produced, for example, 2000·0. This equator and equinox are referred to as the mean equator and mean equinox for 2000·0. Formulas exist, for a time interval of ten years or so, that can provide the mean coordinates (α1, δ1) of a star at the beginning of a year either before or after the reference epoch 2000·0. Thus, if (α, δ) are the mean coordinates of the star at 2000·0, the mean coordinates at 2001·0 are given by
α1 − α = 3·s075 + 1·s336 sin α tan δ
δ1 − δ = 20''·043 cos α. (1)
The problem of computing the changes in the mean coordinates due to precession when the time interval is more than a few years involves a more complicated procedure.
 الاكثر قراءة في النجوم
الاكثر قراءة في النجوم
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


