


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 27-1-2020
Date: 2-2-2016
Date: 30-12-2020
|
Let 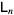 be the
be the 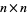 matrix whose
matrix whose 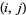 th entry is 1 if
th entry is 1 if 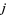 divides
divides 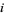 and 0 otherwise, let
and 0 otherwise, let 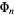 be the
be the 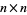 diagonal matrix
diagonal matrix 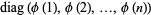 , where
, where 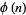 is the totient function, and let
is the totient function, and let 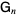 be the
be the 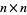 matrix whose
matrix whose 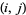 th entry is the greatest common divisor
th entry is the greatest common divisor 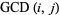 . Then Le Paige's theorem states that
. Then Le Paige's theorem states that
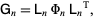 |
where 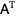 denotes the transpose (Le Paige 1878, Johnson 2003).
denotes the transpose (Le Paige 1878, Johnson 2003).
As a corollary,
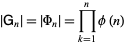 |
(Smith 1876, Johnson 2003). For 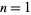 , 2, ... the first few values are 1, 1, 2, 4, 16, 32, 192, 768, ... (OEIS A001088).
, 2, ... the first few values are 1, 1, 2, 4, 16, 32, 192, 768, ... (OEIS A001088).
REFERENCES:
Johnson, W. P. "An 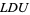 Factorization in Elementary Number Theory." Math. Mag. 76, 392-394, 2003.
Factorization in Elementary Number Theory." Math. Mag. 76, 392-394, 2003.
Le Paige, C. "Sur un théorème de M. Mansion." Nouv. Corresp. Math. 4, 176-178, 1878.
Mansion, P. "On an Arithmetical Theorem of Professor Smith's." Messenger Math. 7, 81-82, 1877.
Muir, T. A Treatise on the Theory of Determinants, Vol. 3. New York: Dover, 1960.
Sloane, N. J. A. Sequence A001088 in "The On-Line Encyclopedia of Integer Sequences."
Smith, H. J. S. "On the Value of a Certain Arithmetical Determinant." Proc. London Math. Soc. 7, 208-212, 1876. Reprinted in The Collected Mathematical Papers of Henry John Stephen Smith, Vol. 2 (Ed. J. W. L. Glaisher). Oxford, England: Clarendon Press, pp. 161-165, 1894.



|
|
|
|
دراسة: حفنة من الجوز يوميا تحميك من سرطان القولون
|
|
|
|
|
|
|
تنشيط أول مفاعل ملح منصهر يستعمل الثوريوم في العالم.. سباق "الأرنب والسلحفاة"
|
|
|
|
|
|
|
لتعزيز التواصل مع الزائرات الأجنبيات : العتبة العلويّة المقدّسة تُطلق دورة لتعليم اللغة الإنجليزية لخادمات القسم النسويّ
|
|
|