
آخر المواضيع المضافة


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 12-9-2020
Date: 30-10-2019
Date: 20-10-2019
|
Define
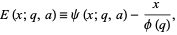 |
(1) |
where
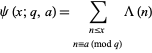 |
(2) |
(Davenport 1980, p. 121), 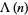 is the Mangoldt function, and
is the Mangoldt function, and 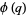 is the totient function. Now define
is the totient function. Now define
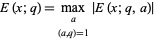 |
(3) |
where the sum is over 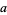 relatively prime to
relatively prime to 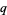 ,
, 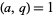 , and
, and
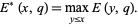 |
(4) |
Bombieri's theorem then says that for fixed 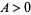 ,
,
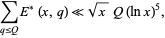 |
(5) |
provided that 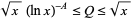 .
.
REFERENCES:
Bombieri, E. "On the Large Sieve." Mathematika 12, 201-225, 1965.
Davenport, H. "Bombieri's Theorem." Ch. 28 in Multiplicative Number Theory, 2nd ed. New York: Springer-Verlag, pp. 161-168, 1980.



|
|
|
|
حقن الذهب في العين.. تقنية جديدة للحفاظ على البصر ؟!
|
|
|
|
|
|
|
علي بابا تطلق نماذج "Qwen" الجديدة في أحدث اختراق صيني لمجال الذكاء الاصطناعي مفتوح المصدر
|
|
|
|
|
|
|
مشاتل الكفيل تنتج أنواعًا مختلفة من النباتات المحلية والمستوردة وتواصل دعمها للمجتمع
|
|
|