


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 3-11-2019
Date: 10-1-2021
Date: 17-10-2019
|

The prime zeta function
 |
(1) |
where the sum is taken over primes is a generalization of the Riemann zeta function
 |
(2) |
where the sum is over all positive integers. In other words, the prime zeta function  is the Dirichlet generating function of the characteristic function of the primes
is the Dirichlet generating function of the characteristic function of the primes  .
.  is illustrated above on positive the real axis, where the imaginary part is indicated in yellow and the real part in red. (The sign difference in the imaginary part compared to the plot appearing in Fröberg is presumably a result of the use of a different convention for
is illustrated above on positive the real axis, where the imaginary part is indicated in yellow and the real part in red. (The sign difference in the imaginary part compared to the plot appearing in Fröberg is presumably a result of the use of a different convention for  .)
.)
Various terms and notations are used for this function. The term "prime zeta function" and notation  were used by Fröberg (1968), whereas Cohen (2000) uses the notation
were used by Fröberg (1968), whereas Cohen (2000) uses the notation  .
.
The series converges absolutely for  , where
, where  , can be analytically continued to the strip
, can be analytically continued to the strip  (Fröberg 1968), but not beyond the line
(Fröberg 1968), but not beyond the line  (Landau and Walfisz 1920, Fröberg 1968) due to the clustering of singular points along the imaginary axis arising from the nontrivial zeros of the Riemann zeta function on the critical line
(Landau and Walfisz 1920, Fröberg 1968) due to the clustering of singular points along the imaginary axis arising from the nontrivial zeros of the Riemann zeta function on the critical line  .
.
As illustrated in the left figure above (where the real part is indicated in red and the imaginary part in yellow), the function has singular points along the real axis for  where
where  runs through all positive integers without a square factor. For
runs through all positive integers without a square factor. For  close to 1,
close to 1,  has the expansion
has the expansion
 |
(3) |
where  and
and
 |
 |
 |
(4) |
 |
 |
 |
(5) |
(OEIS A143524), where  is the Möbius function and
is the Möbius function and  is the Riemann zeta function (Fröberg 1968).
is the Riemann zeta function (Fröberg 1968).

The prime zeta function is plotted above for ![R[s]=1/2](https://mathworld.wolfram.com/images/equations/PrimeZetaFunction/Inline25.gif) and
and ![R[s]=1](https://mathworld.wolfram.com/images/equations/PrimeZetaFunction/Inline26.gif) (Fröberg 1968).
(Fröberg 1968).


The prime zeta function is illustrated above in the complex plane.
The prime zeta function can be expressed in terms of the Riemann zeta function by
![ln[zeta(s)]](https://mathworld.wolfram.com/images/equations/PrimeZetaFunction/Inline27.gif) |
 |
 |
(6) |
 |
 |
 |
(7) |
 |
 |
 |
(8) |
 |
 |
 |
(9) |
Inverting then gives
![P(s)=sum_(k=1)^infty(mu(k))/kln[zeta(ks)]](https://mathworld.wolfram.com/images/equations/PrimeZetaFunction/NumberedEquation4.gif) |
(10) |
(Glaisher 1891, Fröberg 1968, Cohen 2000).
The prime zeta function is implemented in the Wolfram Language as PrimeZetaP[s].
The Dirichlet generating function of the composite numbers  is given by
is given by
 |
 |
 |
(11) |
 |
 |
 |
(12) |
 , The analog of the harmonic series, diverges, but convergence of the series for
, The analog of the harmonic series, diverges, but convergence of the series for  is quadratic. However, dropping the initial term from the sum for
is quadratic. However, dropping the initial term from the sum for  (and adding the Euler-Mascheroni constant
(and adding the Euler-Mascheroni constant  to the result) gives simply the Mertens constant
to the result) gives simply the Mertens constant
 |
 |
 |
(13) |
 |
 |
![gamma+sum_(m=2)^(infty)(mu(m))/mln[zeta(m)]](https://mathworld.wolfram.com/images/equations/PrimeZetaFunction/Inline55.gif) |
(14) |
 |
 |
 |
(15) |
(OEIS A077761).
Artin's constant  is connected with
is connected with  by
by
 |
(16) |
where  is a Lucas number (Ribenboim 1998, Gourdon and Sebah).
is a Lucas number (Ribenboim 1998, Gourdon and Sebah).
The values of  for the first few integers
for the first few integers  starting with two are given in the following table. Merrifield (1881) computed
starting with two are given in the following table. Merrifield (1881) computed  for
for  up to 35 to 15 digits, and Liénard (1948) computed
up to 35 to 15 digits, and Liénard (1948) computed  up to
up to  to 50 digits (Ribenboim 1996). Gourdon and Sebah give values to 60 digits for
to 50 digits (Ribenboim 1996). Gourdon and Sebah give values to 60 digits for  .
.
 |
OEIS |  |
| 2 | A085548 | 0.452247 |
| 3 | A085541 | 0.174763 |
| 4 | A085964 | 0.0769931 |
| 5 | A085965 | 0.035755 |
| 6 | A085966 | 0.0170701 |
| 7 | A085967 | 0.00828383 |
| 8 | A085968 | 0.00406141 |
| 9 | A085969 | 0.00200447 |
| 10 | 0.000993604 |

According to Fröberg (1968), very little is known about the roots  . The plots above show the positions of zeros (left figure) and contours of zero real (red) and imaginary (blue) parts in a portion of the complex plane, with roots indicated as black dots (right figure).
. The plots above show the positions of zeros (left figure) and contours of zero real (red) and imaginary (blue) parts in a portion of the complex plane, with roots indicated as black dots (right figure).
REFERENCES:
Cohen, H. "High Precision Computation of Hardy-Littlewood Constants." Preprint. http://www.math.u-bordeaux.fr/~cohen/hardylw.dvi.
Cohen, H. Advanced Topics in Computational Number Theory. New York: Springer-Verlag, 2000.
Dahlquist, G. "On the Analytic Continuation of Eulerian Products." Arkiv för Math. 1, 533-554, 1951.
Davis, H. T. Tables of the Higher Mathematical Functions, Vol. 2. Bloomington, IN: Principia Press, p. 249, 1933.
Fröberg, C.-E. "On the Prime Zeta Function." BIT 8, 187-202, 1968.
Glaisher, J. W. L. "On the Sums of Inverse Powers of the Prime Numbers." Quart. J. Math. 25, 347-362, 1891.
Gourdon, X. and Sebah, P. "Some Constants from Number Theory." http://numbers.computation.free.fr/Constants/Miscellaneous/constantsNumTheory.html.
Hardy, G. H. and Wright, E. M. An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Oxford University Press, pp. 355-356, 1979.
Haselgrove, C. B. and Miller, J. C. P. "Tables of the Riemann Zeta Function." Royal Society Mathematical Tables, Vol. 6. Cambridge, England: Cambridge University Press, p. 58, 1960.
Landau, E. and Walfisz, A. "Über die Nichfortsetzbarkeit einiger durch Dirichletsche Reihen definierter Funktionen." Rend. Circ. Math. Palermo 44, 82-86, 1920.
Liénard, R. Tables fondamentales à 50 décimales des sommes  ,
,  ,
, 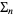 . Paris: Centre de Docum. Univ., 1948.
. Paris: Centre de Docum. Univ., 1948.
Merrifield, C. W. "The Sums of the Series of Reciprocals of the Prime Numbers and of Their Powers." Proc. Roy. Soc. London 33, 4-10, 1881.
Muñoz García, E. and Pérez Marco, R. "The Product Over All Primes is 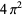 ." Preprint IHES/M/03/34. May 2003. http://inc.web.ihes.fr/prepub/PREPRINTS/M03/Resu/resu-M03-34.html.
." Preprint IHES/M/03/34. May 2003. http://inc.web.ihes.fr/prepub/PREPRINTS/M03/Resu/resu-M03-34.html.
Muñoz García, E. and Pérez Marco, R. "The Product Over All Primes is 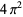 ." Commun. Math. Phys. 277, 69-81, 2008.
." Commun. Math. Phys. 277, 69-81, 2008.
Ribenboim, P. The New Book of Prime Number Records. New York: Springer-Verlag, 1996.
Sloane, N. J. A. Sequences A077761, A085541, A085548, A085964, A085965, A085966, A085967, A085968, A085969, and A143524 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
دراسة: حفنة من الجوز يوميا تحميك من سرطان القولون
|
|
|
|
|
|
|
تنشيط أول مفاعل ملح منصهر يستعمل الثوريوم في العالم.. سباق "الأرنب والسلحفاة"
|
|
|
|
|
|
|
لتعزيز التواصل مع الزائرات الأجنبيات : العتبة العلويّة المقدّسة تُطلق دورة لتعليم اللغة الإنجليزية لخادمات القسم النسويّ
|
|
|