Octahedral Number

A figurate number which is the sum of two consecutive pyramidal numbers,

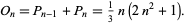(1)

The first few are 1, 6, 19, 44, 85, 146, 231, 344, 489, 670, 891, 1156, ... (OEIS A005900). The generating function for the octahedral numbers is

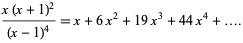(2)

Pollock (1850) conjectured that every number is the sum of at most 7 octahedral numbers (Dickson 2005, p. 23).

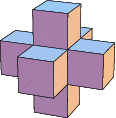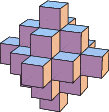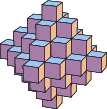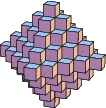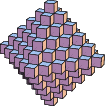A related set of numbers is the number of cubes in the Haűy construction of the octahedron. Each cross section has area

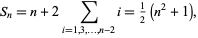(3)

where  is an odd number, and adding all cross sections gives

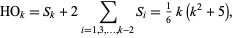(4)

for 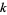 an odd number. Re-indexing so that  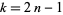gives

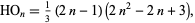(5)

the first few values of which are 1, 7, 25, 63, 129, ... (OEIS A001845). These numbers have the generating function

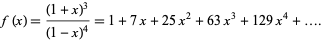(6)

REFERENCES:

Conway, J. H. and Guy, R. K. The Book of Numbers. New York: Springer-Verlag, p. 50, 1996.

Dickson, L. E. History of the Theory of Numbers, Vol. 2: Diophantine Analysis. New York: Dover, 2005.

Pollock, F. "On the Extension of the Principle of Fermat's Theorem of the Polygonal Numbers to the Higher Orders of Series Whose Ultimate Differences Are Constant. With a New Theorem Proposed, Applicable to All the Orders." Abs. Papers Commun. Roy. Soc. London 5, 922-924, 1843-1850.

Sloane, N. J. A. Sequences A001845/M4384 and A005900/M4128 in "The On-Line Encyclopedia of Integer Sequences."