طريقة الاضطراب المعكوس IPA

كل الطرق الانفة الذكر لتعيين منحنيات الجهد تستخدم مجموعة من الثوابت الجزيئية التي يتم تعيينها بملائمة المربعات الصغرى least-square fit لقيم الحد الطيفي المقاسة T (v,J) وبمساعدة هذه المجموعة من الثوابت يتعين الجهد (E_pot(r اما بواسطة متوالية اسية ترتبط مكافئاتها بالثوابت الفيزيائية او بحساب نقاط التحول الكلاسيكية للاهتزاز وايجاد منحني الجهد نقطة بعد نقطة.

ان الثوابت الجزيئية ليست احادية التعيين بشكل عام لوجود علاقات ارتباط بينها ولتاكيد احادية الثوابت الجزيئية واعطائها معنى فيزيائي واضح نحتاج لايجاد ثوابت لا تسمح فقط باعادة تكوين الحد الطيفي والتنبؤ بالمجهول منها فقط ولكن تخضع ايضا للشروط الحدودية لهاملتون النظام الجزيئي قيد الدراسة.

وطريقة الاضطراب المعكوس المقترحة من قبل كوسمان Kosman وهاينز Hinze مبنية على مبدأ التغير variational principle وتخضع للمتطلبات المذكورة اعلاه افضل كثيرا من الطرق الاخرى وجرى تطوير هذه الطريقة من قبل فيدال Vidal الى اجراءات عددية للتعيين الدقيق للثوابت الجزيئية ومنحنيات الجهد ويستخدم اجراء IPA طريقة تحسين الحلول optimization لجهد جزيئة غير دوارة من معادلة شرودنجر:

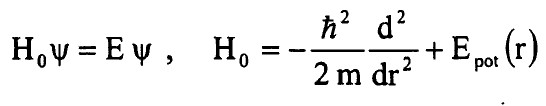...........(1)

وتوصف الجزيئة الدوارة بمعادلة شرودنجر:

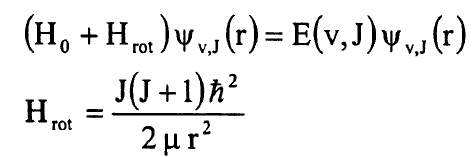.......(2)

بواسطة طريقة التغير يتم تحسين قيمة (E_pot(r الى ان تتفق قيم الطاقات المقاسة E(v,J) مع القيم المحسوبة من المعادلة (2).

تبدأ من:

...........(3)

حيث (E_pot(r هو جهد نقطة البداية (مثل جهد RKR المعين من مكافئات دنهام) و(ΔE_pot(r حد تصخحيح ويكمن الحصول على تصحيح الطاقة ΔE_v,J من حساب رتبة الاضطراب الاولى من خلال:

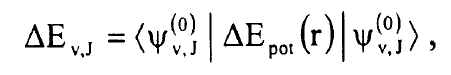........(4)

حيث الدوال غير المضطربة ⁽Ψ⁽⁰ هي حلول معادلة نقطة البداية:

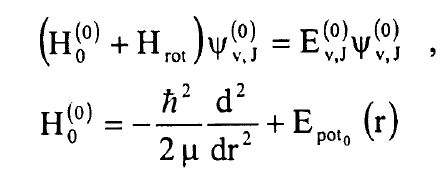..........(5)

وعلى التباين من طريقة الاضطراب الاعتيادية حيث تحسب تصحيحات الطاقة ΔE لاضطراب معطى (ΔE_pot(r من فروق الطاقة:

.............(6)

بين القيم التجريبية E^exp_v,J والطاقات E⁽⁰⁾_v,J المحسوبة من معادلة نقطة البداية واذا كان جهد نقطة البداية (E_pot(r جيدا فان حساب اضطراب الرتبة الاولى يكفي لتعيين (ΔE_pot(r من الممكن الحصول على طريقة تكرار باستخدام الجهد الذي تم الحصول عليه في خطوة التقريب الاولى كجهد نقطة البداية للخطوة الثانية، الخ وان الشكل المختار لفرق الطاقة (ΔE_pot(r له اهمية كبيرة للوصول الى تقارب سريع للتكرار وقد تبين ان التراكب الخطي لحاصل ضرب متعددة حدود ليجندر (P_i(x ودوال جاوس:

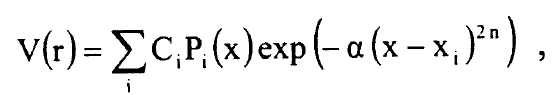.............(7)

يعطي افضل النتائج للتكامل العددي لمعادلة شرودنجر وقيمة الأس n تكون في حدود 1≤ n ≥​5 ومقدار x للدوال P ولدوال جاوس تتعين بالمسافة بين النوى ونقاط التحول الداخلية والخارجية في الجهد (E_pot(r ومعرف بالمعادلة:

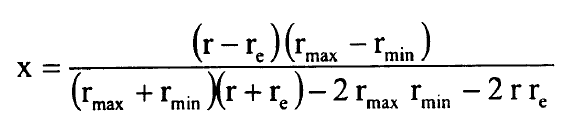...........(8)

لذلك x = 1 عندما r = r_max، x=-1 عندما r=r_min وx=0 عندما r=r_e. يمكن حساب قيم الحد الطيفي G(v) في الجهد المتعين بالتكرار E_pot(r) كقيم ذاتية لمعادلة شرودنجر (1) للجزيئة الدوارة:

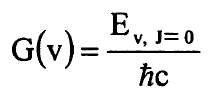..............(9)

والثابت الدوراني B(v) معطى بالقيمة المتوقعة:

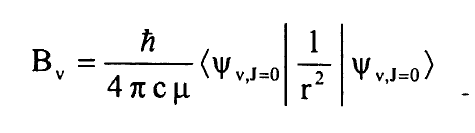............(10)

حيث يكمن تعيين الثوابت الاهتزازية بالتكرار العددي.

اخر الاخبار

اخبار العتبة العباسية المقدسة

قسم الشؤون الفكرية يطلق باقة من النشاطات الرقمية الخاصة بشهر المحرم

العتبة العباسية المقدسة تختتم السلسلة الأولى لمشروع المحاضرات القرآنية العاشورائية في بابل

العتبة العباسية المقدسة تسلّم راية العزاء إلى تجمّع مواكب محافظة الديوانية

قسم الشؤون الفكرية يواصل إقامة المجالس الحسينية ضمن سلسلة (بيوت النعيم)

المزيد

الآخبار الصحية

تناول الجبن.. مفيد للجسم أم خطر يهدد صحتك؟

طبيبة أسنان تحذر.. لا تتجاهل هذه العلامة بعد التنظيف

يجب أن تأكل المزيد من الشمام هذا الصيف.. إليك السبب ؟

تأثير صحي كبير.. كم بيضة يجب أن تتناول يوميا؟

المزيد

الآخبار التكنلوجية

أداء خلايا البيروفسكايت الشمسية تحت الماء قد يزيد كفاءة تحويل الكهرباء

مسافة الأمان: أساس القيادة الآمنة وتجنب الحوادث

هل القيادة السريعة تعني استهلاك اكثر للوقود؟

لماذا يعتبر كوكب المريخ غير صالح للحياة؟

المزيد

مواضيع ذات صلة

الكشف عن الألغام والمتفجرات

الكربون .. أمير المواد وعميدها

خواص المواد النانوية

تاريخ أنابيب الكربون النانوية (History of carbon nanotubes)

الاتصال والحوار العام في تطوير تقنية النانو

نشاطات المنظمات الدولية في مجال التقنية النانوية

حالة المعارف المتصلة بمخاطر المواد النانوية

الاعتبارات الأخلاقية في التقنية النانويه

المنفعة الاجتماعية للتقنية النانوية

ما المقصود بالنانو؟

النانو تكنولوجيا.. علم وصناعة القرن الجديد

أنابيب الكربون النانوية Nanotubes Carbon