Random Walk--3-Dimensional

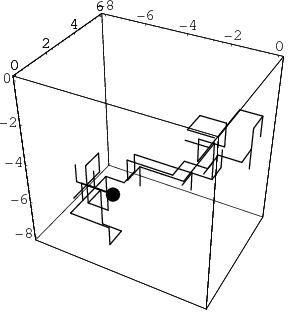
On a three-dimensional lattice, a random walk has less than unity probability of reaching any point (including the starting point) as the number of steps approaches infinity. The probability of reaching the starting point again is 0.3405373296.... This is one of Pólya's random walk constants.

REFERENCES:

Glasser, M. L. and Zucker, I. J. "Extended Watson Integrals for the Cubic Lattices." Proc. Nat. Acad. Sci. U.S.A. 74, 1800-1801, 1977.

McCrea, W. H. and Whipple, F. J. W. "Random Paths in Two and Three Dimensions." Proc. Roy. Soc. Edinburgh 60, 281-298, 1940.

Trott, M. "The Mathematica Guidebooks Additional Material: Lattice Sites Visited by Random Walkers." https://www.mathematicaguidebooks.org/additions.shtml#S_2_04.