Rayleigh Distribution

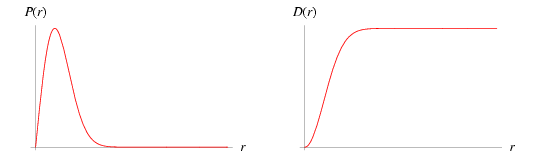
The distribution with probability density function and distribution function

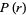			(1)
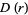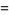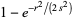			(2)

for 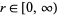 and parameter .

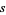It is implemented in the Wolfram Language as RayleighDistribution[s].

The raw moments are given by

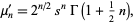(3)

where 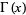 is the gamma function, giving the first few as

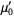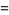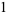			(4)
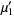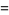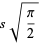			(5)
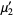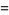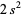			(6)
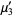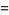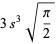			(7)
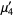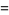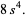			(8)

The central moments are therefore

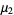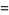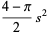			(9)
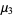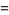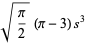			(10)
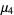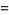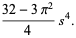			(11)

The mean, variance, skewness, and kurtosis excess are

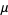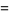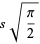			(12)
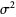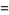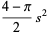			(13)
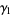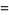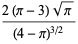			(14)
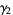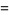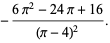			(15)

The characteristic function is

(16)

REFERENCES:

Papoulis, A. Probability, Random Variables, and Stochastic Processes, 2nd ed. New York: McGraw-Hill, pp. 104 and 148, 1984.