


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 13-4-2021
Date: 6-2-2021
Date: 10-4-2021
|
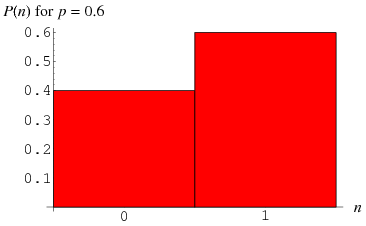
The Bernoulli distribution is a discrete distribution having two possible outcomes labelled by 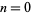 and
and 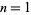 in which
in which 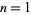 ("success") occurs with probability
("success") occurs with probability 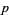 and
and 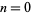 ("failure") occurs with probability
("failure") occurs with probability 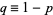 , where
, where 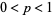 . It therefore has probability density function
. It therefore has probability density function
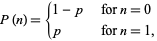 |
(1) |
which can also be written
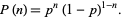 |
(2) |
The corresponding distribution function is
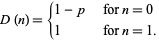 |
(3) |
The Bernoulli distribution is implemented in the Wolfram Language as BernoulliDistribution[p].
The performance of a fixed number of trials with fixed probability of success on each trial is known as a Bernoulli trial.
The distribution of heads and tails in coin tossing is an example of a Bernoulli distribution with 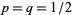 . The Bernoulli distribution is the simplest discrete distribution, and it the building block for other more complicated discrete distributions. The distributions of a number of variate types defined based on sequences of independent Bernoulli trials that are curtailed in some way are summarized in the following table (Evans et al. 2000, p. 32).
. The Bernoulli distribution is the simplest discrete distribution, and it the building block for other more complicated discrete distributions. The distributions of a number of variate types defined based on sequences of independent Bernoulli trials that are curtailed in some way are summarized in the following table (Evans et al. 2000, p. 32).
| distribution | definition |
| binomial distribution | number of successes in 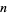 trials trials |
| geometric distribution | number of failures before the first success |
| negative binomial distribution | number of failures before the  th success th success |
The characteristic function is
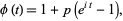 |
(4) |
and the moment-generating function is
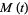 |
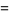 |
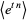 |
(5) |
 |
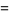 |
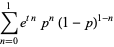 |
(6) |
 |
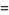 |
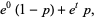 |
(7) |
so
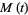 |
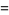 |
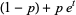 |
(8) |
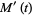 |
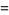 |
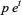 |
(9) |
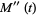 |
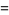 |
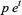 |
(10) |
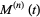 |
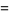 |
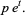 |
(11) |
These give raw moments
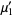 |
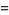 |
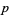 |
(12) |
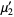 |
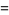 |
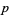 |
(13) |
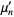 |
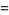 |
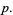 |
(14) |
and central moments
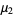 |
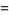 |
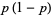 |
(15) |
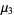 |
 |
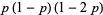 |
(16) |
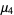 |
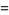 |
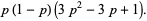 |
(17) |
The mean, variance, skewness, and kurtosis excess are then
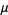 |
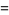 |
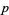 |
(18) |
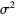 |
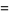 |
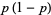 |
(19) |
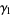 |
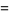 |
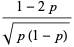 |
(20) |
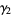 |
 |
 |
(21) |
To find an estimator 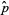 for the mean of a Bernoulli population with population mean
for the mean of a Bernoulli population with population mean 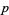 , let
, let 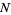 be the sample size and suppose
be the sample size and suppose 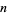 successes are obtained from the
successes are obtained from the 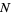 trials. Assume an estimator given by
trials. Assume an estimator given by
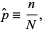 |
(22) |
so that the probability of obtaining the observed 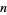 successes in
successes in 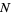 trials is then
trials is then
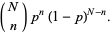 |
(23) |
The expectation value of the estimator 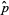 is therefore given by
is therefore given by
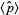 |
 |
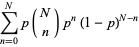 |
(24) |
 |
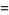 |
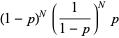 |
(25) |
 |
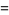 |
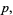 |
(26) |
so 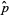 is indeed an unbiased estimator for the population mean
is indeed an unbiased estimator for the population mean 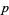 .
.
The mean deviation is given by
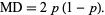 |
(27) |
REFERENCES:
Evans, M.; Hastings, N.; and Peacock, B. "Bernoulli Distribution." Ch. 4 in Statistical Distributions, 3rd ed. New York: Wiley, pp. 31-33, 2000.



|
|
|
|
دراسة: حفنة من الجوز يوميا تحميك من سرطان القولون
|
|
|
|
|
|
|
تنشيط أول مفاعل ملح منصهر يستعمل الثوريوم في العالم.. سباق "الأرنب والسلحفاة"
|
|
|
|
|
|
|
تثميناً لجهودهم.. العتبة العباسية المقدسة تكرِّم اللجنة التحكيمية والجهات المساهمة بمسابقة فنِّ الخطابة
|
|
|