
Rule 102
 المؤلف:
Sloane, N. J. A.
المؤلف:
Sloane, N. J. A.
 المصدر:
Sequences A001317/M2495, A047999, A075439, and A117998 in "The On-Line Encyclopedia of Integer Sequences."
المصدر:
Sequences A001317/M2495, A047999, A075439, and A117998 in "The On-Line Encyclopedia of Integer Sequences."
 الجزء والصفحة:
...
الجزء والصفحة:
...
 25-8-2021
25-8-2021
 1867
1867
Rule 102
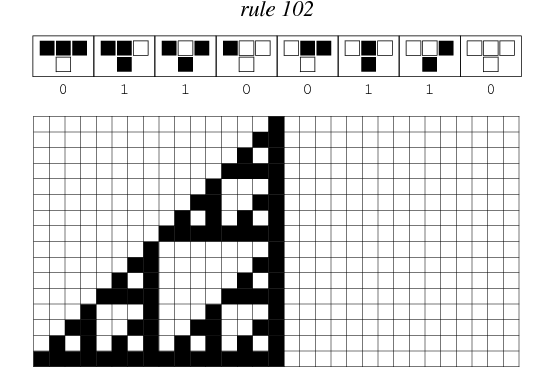
Rule 102 is one of the elementary cellular automaton rules introduced by Stephen Wolfram in 1983 (Wolfram 1983, 2002). It specifies the next color in a cell, depending on its color and its immediate neighbors. Its rule outcomes are encoded in the binary representation 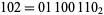 . This rule is illustrated above together with the evolution of a single black cell it produces after 15 steps (OEIS A075439; Wolfram 2002, p. 55).
. This rule is illustrated above together with the evolution of a single black cell it produces after 15 steps (OEIS A075439; Wolfram 2002, p. 55).
Starting with a single black cell, successive generations are given by interpreting the numbers 1, 6, 20, 120, 272, 1632, 5440, 32640, ... (OEIS A117998) in binary. Omitting trailing zeros (the right  cells in step
cells in step  of the triangle are always 0) gives 1, 3, 5, 15, 17, 51, 85, 255, 257, 771, ... (OEIS A001317), which are simply the previous numbers divided by
of the triangle are always 0) gives 1, 3, 5, 15, 17, 51, 85, 255, 257, 771, ... (OEIS A001317), which are simply the previous numbers divided by 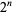 and which have binary representation 1, 11; 101, 1111, 10001, ... (OEIS A047999). Surprisingly, this is precisely the Sierpiński sieve.
and which have binary representation 1, 11; 101, 1111, 10001, ... (OEIS A047999). Surprisingly, this is precisely the Sierpiński sieve.
The mirror image is rule 60, the complement is rule 153, and the mirrored complement is rule 195.
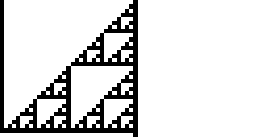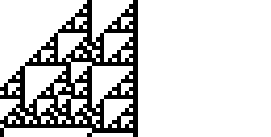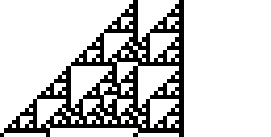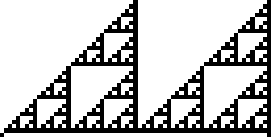
Rule 102 is one of the eight additive elementary cellular automata (Wolfram 2002, p. 953).
REFERENCES:
Sloane, N. J. A. Sequences A001317/M2495, A047999, A075439, and A117998 in "The On-Line Encyclopedia of Integer Sequences."
Wolfram, S. "Statistical Mechanics of Cellular Automata." Rev. Mod. Phys. 55, 601-644, 1983.
Wolfram, S. A New Kind of Science. Champaign, IL: Wolfram Media, pp. 55, 90, and 953, 2002.
 الاكثر قراءة في الرياضيات التطبيقية
الاكثر قراءة في الرياضيات التطبيقية
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


