The Lorenz attractor is an attractor that arises in a simplified system of equations describing the two-dimensional flow of fluid of uniform depth , with an imposed temperature difference 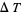, under gravity 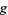, with buoyancy 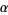, thermal diffusivity 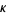, and kinematic viscosity . The full equations are

			(1)
			(2)

Here, 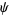 is a stream function, defined such that the velocity components  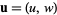of the fluid motion are

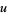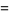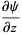			(3)
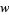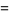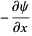			(4)

(Tabor 1989, p. 205).

In the early 1960s, Lorenz accidentally discovered the chaotic behavior of this system when he found that, for a simplified system, periodic solutions of the form

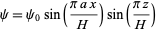(5)

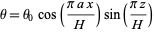(6)

grew for Rayleigh numbers larger than the critical value, 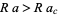. Furthermore, vastly different results were obtained for very small changes in the initial values, representing one of the earliest discoveries of the so-called butterfly effect.

Lorenz included the terms

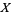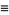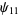			(7)
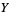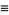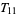			(8)
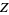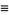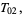			(9)

where 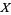 is proportional to convective intensity,  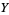to the temperature difference between descending and ascending currents, and  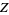to the difference in vertical temperature profile from linearity in his system of equations. From these, he obtained the simplified equations

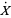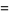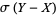			(10)
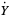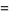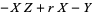			(11)
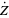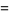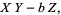			(12)

now known as the Lorenz equations. Here, 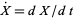, , 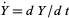, 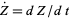and

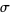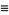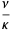			(13)
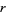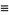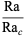			(14)
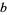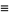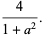			(15)

where 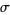 is the Prandtl number, Ra is the Rayleigh number,  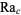is the critical Rayleigh number, and  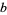is a geometric factor (Tabor 1989, p. 206). Lorenz took  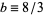and .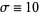

The Lorenz attractor has a correlation exponent of 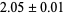 and capacity dimension  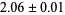(Grassberger and Procaccia 1983). For more details, see Lichtenberg and Lieberman (1983, p. 65) and Tabor (1989, p. 204). As one of his list of challenging problems for mathematics (Smale's problems), Smale (1998, 2000) posed the open question of whether the Lorenz attractor is a strange attractor. This question was answered in the affirmative by Tucker (2002), whose technical proof makes use of a combination of normal form theory and validated interval arithmetic.

The critical points at (0, 0, 0) correspond to no convection, and the critical points at

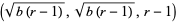(16)

and

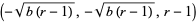(17)

correspond to steady convection. This pair is stable only if

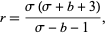(18)

which can hold only for positive 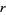 if .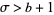

The image above shows a Lorenz attractor laser-etched into glass by digital sculptor Bathsheba Grossman (http://www.bathsheba.com/).

REFERENCES:

Gleick, J. Chaos: Making a New Science. New York: Penguin Books, pp. 27-31, center plate (following p. 114), and p. 140, 1988.

Grassberger, P. and Procaccia, I. "Measuring the Strangeness of Strange Attractors." Physica D 9, 189-208, 1983.

Grossman, B. "Lorenz Attractor Crystal." http://www.bathsheba.com/crystalsci/lorenz/.

Guckenheimer, J. "A Strange, Strange Attractor." In The Hopf Bifurcation and Its Applications (Ed. J. E. Marsden and M. McCracken). New York: Springer-Verlag, 1976.

Guckenheimer, J. and Williams, R. F. "Structural Stability of Lorenz Attractors." Publ. Math. IHES 50, 307-320, 1979.

Lichtenberg, A. and Lieberman, M. Regular and Stochastic Motion. New York: Springer-Verlag, 1983.

Lorenz, E. N. "Deterministic Nonperiodic Flow." J. Atmos. Sci. 20, 130-141, 1963.

Lorenz, E. N. "On the Prevalence of Aperiodicity in Simple Systems." In Global Analysis: Proceedings of the Biennial Seminar of the Canadian Mathematical Congress Held at the University of Calgary, Alberta, June 12-27 (Ed. M. Grmela and J. E. Marsden). New York: Springer-Verlag, pp. 53-75, 1979.

Peitgen, H.-O.; Jürgens, H.; and Saupe, D. Chaos and Fractals: New Frontiers of Science. New York: Springer-Verlag, pp. 697-708, 1992.

Rand, D. "The Topological Classification of Lorenz Attractors." Math. Proc. Cambridge Philos. Soc. 83, 451-460, 1978.

Smale, S. "Mathematical Problems for the Next Century." Math. Intelligencer 20, No. 2, 7-15, 1998.

Smale, S. "Mathematical Problems for the Next Century." In Mathematics: Frontiers and Perspectives 2000 (Ed. V. Arnold, M. Atiyah, P. Lax, and B. Mazur). Providence, RI: Amer. Math. Soc., 2000.

Sparrow, C. The Lorenz Equations: Bifurcations, Chaos, and Strange Attractors. New York: Springer-Verlag, 1982.

Stewart, I. "The Lorenz Attractor Exists." Nature 406, 948-949, 2000.

Tabor, M. Chaos and Integrability in Nonlinear Dynamics: An Introduction. New York: Wiley, 1989.

Tucker, W. "A Rigorous ODE Solver and Smale's 14th Problem." Found. Comput. Math. 2, 53-117, 2002.

Viana, M. "What's New on Lorenz Strange Attractors." Math. Intell. 22, 6-19.

Weisstein, E. W. "Smale's 14th Problem Solved." MathWorld Headline News, Feb. 13, 2002. http://mathworld.wolfram.com/news/2002-02-13/smale14th/.

Wells, D. The Penguin Dictionary of Curious and Interesting Geometry. London: Penguin, pp. 142-143, 1991.

Williams, R. F. "The Structure of Lorenz Attractors." Publ. Math. IHES 50, 321-347, 1979.

Yorke, J. A. and Yorke, E. D. "Metastable Chaos: The Transition to Sustained Chaotic Oscillation in a Model of Lorenz." J. Stat. Phys. 21, 263-277, 1979.

اخر الاخبار

اخبار العتبة العباسية المقدسة

قسم الشؤون الطبية يقدم الخدمات الصحية والعلاجية لزائري مدينة سامراء

العتبة العباسية المقدسة تقدم خدماتها لزائري مرقد الإمامين العسكريين (عليهما السلام) في سامراء

المجمَع العلمي ووفد وزارة التربية يبحثان سبل التعاون المشترك

قسم الشؤون الفكرية يصدر العدد 192 من مجلة الرياحين للأطفال

المزيد

الآخبار الصحية

كنز غذائي على طبقك.. ماذا تفعل السبانخ بجسمك؟

ما لا يتوقعه أحد.. "سر غذائي" في الجبن الدسم

لتحسين الهضم والنوم.. هذا أفضل وقت لتناول العشاء

10 طرق بسيطة وغير مألوفة لحرق المزيد من السعرات يوميا

المزيد

الآخبار التكنلوجية

سابقة بعالم الطيران.. طائرة تقرر الهبوط بنفسها بعد ظرف طارئ

"الإنفلونزا الخارقة" تكتسح دول العالم.. وتثير قلقا كبيرا

مرحلة ما قبل الأعراض.. دواء جديد يستهدف "شرارة" الزهايمر

إزالة ثاني أكسيد الكربون من الغلاف الجوي.. ما دور المحيطات والبحار؟

المزيد