

النبات

مواضيع عامة في علم النبات

الجذور - السيقان - الأوراق

النباتات الوعائية واللاوعائية

البذور (مغطاة البذور - عاريات البذور)

الطحالب

النباتات الطبية


الحيوان

مواضيع عامة في علم الحيوان

علم التشريح

التنوع الإحيائي

البايلوجيا الخلوية


الأحياء المجهرية

البكتيريا

الفطريات

الطفيليات

الفايروسات


علم الأمراض

الاورام

الامراض الوراثية

الامراض المناعية

الامراض المدارية

اضطرابات الدورة الدموية

مواضيع عامة في علم الامراض

الحشرات


التقانة الإحيائية

مواضيع عامة في التقانة الإحيائية


التقنية الحيوية المكروبية

التقنية الحيوية والميكروبات

الفعاليات الحيوية

وراثة الاحياء المجهرية

تصنيف الاحياء المجهرية

الاحياء المجهرية في الطبيعة

أيض الاجهاد

التقنية الحيوية والبيئة

التقنية الحيوية والطب

التقنية الحيوية والزراعة

التقنية الحيوية والصناعة

التقنية الحيوية والطاقة

البحار والطحالب الصغيرة

عزل البروتين

هندسة الجينات


التقنية الحياتية النانوية

مفاهيم التقنية الحيوية النانوية

التراكيب النانوية والمجاهر المستخدمة في رؤيتها

تصنيع وتخليق المواد النانوية

تطبيقات التقنية النانوية والحيوية النانوية

الرقائق والمتحسسات الحيوية

المصفوفات المجهرية وحاسوب الدنا

اللقاحات

البيئة والتلوث


علم الأجنة

اعضاء التكاثر وتشكل الاعراس

الاخصاب

التشطر

العصيبة وتشكل الجسيدات

تشكل اللواحق الجنينية

تكون المعيدة وظهور الطبقات الجنينية

مقدمة لعلم الاجنة


الأحياء الجزيئي

مواضيع عامة في الاحياء الجزيئي


علم وظائف الأعضاء


الغدد

مواضيع عامة في الغدد

الغدد الصم و هرموناتها

الجسم تحت السريري

الغدة النخامية

الغدة الكظرية

الغدة التناسلية

الغدة الدرقية والجار الدرقية

الغدة البنكرياسية

الغدة الصنوبرية

مواضيع عامة في علم وظائف الاعضاء

الخلية الحيوانية

الجهاز العصبي

أعضاء الحس

الجهاز العضلي

السوائل الجسمية

الجهاز الدوري والليمف

الجهاز التنفسي

الجهاز الهضمي

الجهاز البولي


المضادات الميكروبية

مواضيع عامة في المضادات الميكروبية

مضادات البكتيريا

مضادات الفطريات

مضادات الطفيليات

مضادات الفايروسات

علم الخلية

الوراثة

الأحياء العامة

المناعة

التحليلات المرضية

الكيمياء الحيوية

مواضيع متنوعة أخرى

الانزيمات
Michaelis-Menten Kinetics
المؤلف:
Denise R. Ferrier
المصدر:
Lippincott Illustrated Reviews: Biochemistry
الجزء والصفحة:
6-9-2021
2539
Michaelis-Menten Kinetics
Leonor Michaelis and Maude Menten proposed a simple model that accounts for most of the features of many enzyme-catalyzed reactions. In this model, the enzyme reversibly combines with its substrate to form an ES complex that subsequently yields product, regenerating the free enzyme. The reaction model, involving one substrate molecule, is represented below:
where S is the substrate.
E is the enzyme.
ES is the enzyme–substrate complex.
P is the product.
k1, k−1, and k2 (or, kcat) are rate constants.
A. Michaelis-Menten equation
The Michaelis-Menten equation describes how reaction velocity varies with substrate concentration:
where vo = initial reaction velocity
Vmax = maximal velocity = kcat [E]Total
Km = Michaelis constant = (k−1 + k2)/k1
[S] = substrate concentration
The following assumptions are made in deriving the Michaelis-Menten rate equation.
1. Enzyme and substrate relative concentrations: The substrate concentration ([S]) is much greater than the concentration of enzyme so that the percentage of total substrate bound by the enzyme at any one time is small.
2. Steady-state assumption: The concentration of the ES complex does not change with time (the steady-state assumption), that is, the rate of formation of ES is equal to that of the breakdown of ES (to E + S and to E + P). In general, an intermediate in a series of reactions is said to be in steady state when its rate of synthesis is equal to its rate of degradation.
3. Initial velocity: Initial reaction velocities (vo) are used in the analysis of enzyme reactions. This means that the rate of the reaction is measured as soon as enzyme and substrate are mixed. At that time, the concentration of product is very small, and therefore, the rate of the back reaction from product to substrate can be ignored.
B. Important conclusions
1. Km characteristics: Km, the Michaelis constant, is characteristic of an enzyme and its particular substrate and reflects the affinity of the enzyme for that substrate. Km is numerically equal to the substrate concentration at which the reaction velocity is equal to one half Vmax. Km does not vary with enzyme concentration.
a. Small Km: A numerically small (low) Km reflects a high affinity of the enzyme for substrate, because a low concentration of substrate is needed to half-saturate the enzyme—that is, to reach a velocity that is one half Vmax (Fig. 1).
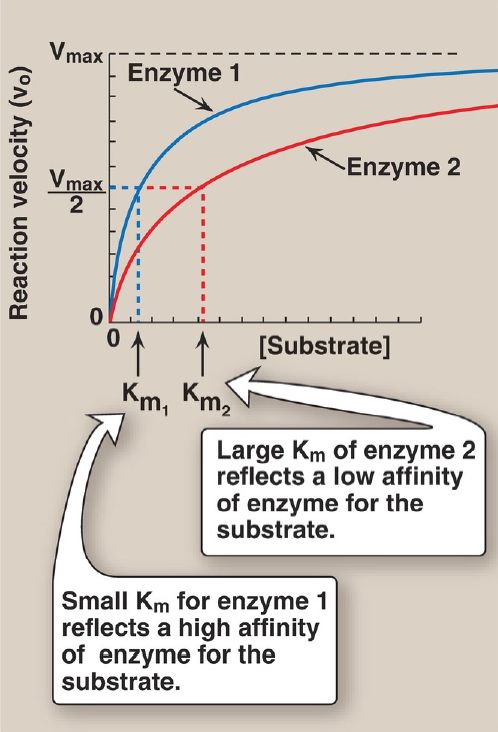
Figure 1 Effect of substrate concentration on reaction velocities for two enzymes: enzyme 1 with a small Michaelis constant (Km) and enzyme 2 with a large Km. Vmax = maximal velocity.
b. Large Km: A numerically large (high) Km reflects a low affinity of enzyme for substrate because a high concentration of substrate is needed to half-saturate the enzyme.
2. Velocity relationship to enzyme concentration: The rate of the reaction is directly proportional to the enzyme concentration because [S] is not limiting. For example, if the enzyme concentration is halved, the initial rates of the reaction (vo) and that of Vmax are reduced to half that of the original.
3. Reaction order: When [S] is much less (<<) than Km, the velocity of the reaction is approximately proportional to the substrate concentration (Fig. 2). The rate of reaction is then said to be first order with respect to substrate. When [S] is much greater (>>) than Km, the velocity is constant and equal to Vmax. The rate of reaction is then independent of substrate concentration (the enzyme is saturated with substrate) and is said to be zero order with respect to substrate concentration (see Fig. 2).
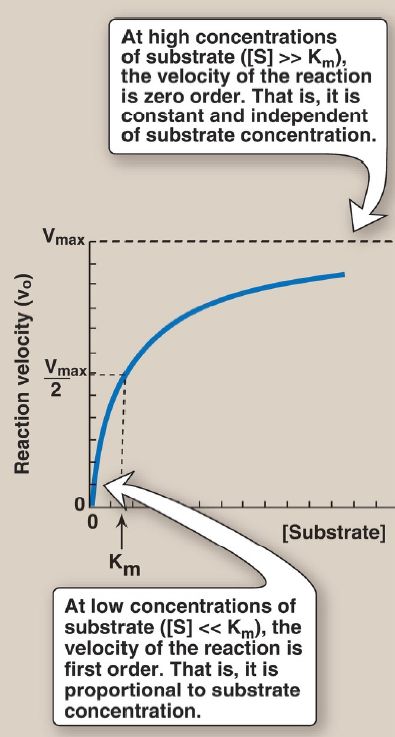
Figure 2 Effect of substrate concentration on reaction velocity for an enzymecatalyzed reaction. Vmax = maximal velocity; Km = Michaelis constant.
 الاكثر قراءة في الكيمياء الحيوية
الاكثر قراءة في الكيمياء الحيوية
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















