

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
خلاصة دراسة منحنى الدالة y = f(x) في المجال [a , b] : CONCLUSION OF STUDY OF FUNCTION GRAPH IN INTERVAL [ A , B]
المؤلف:
د.لحسن عبدالله باشيوة
المصدر:
الرياضيات الاساسية وتطبيقاتها
الجزء والصفحة:
30-37
2-11-2021
6170
خلاصة دراسة منحنى الدالة y = f(x) في المجال [a , b] :
CONCLUSION OF STUDY OF FUNCTION GRAPH IN INTERVAL [ A , B]
خطوات تمثيل الدوال : Graph study process
الخطوة الأولى Case One : في الأول يتم التعرف على صيغة الدالة ومداها ، ثم رسم معلم متعامد ، وإن أمكن متجانس على الورقة المليمترية. من بين المعالم المطلوب معرفتها على مستوى المقرر ثلاثة وهي :
1- معلم ذو محورين (OX , OY) ، وهو المعلم المألوف في المستوى.
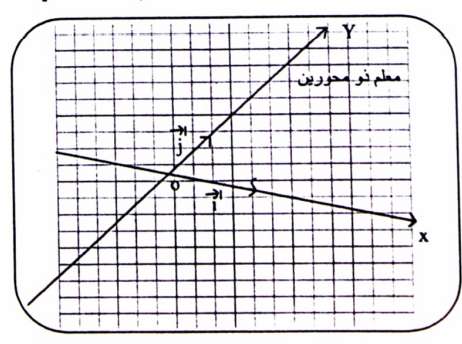
شكل (1-1)
2- معلم متعامد ذو محورين (O , X , Y , I , J) ، وهو معلم كثير الاستخدام في المستوى لتمثيل البيانات.
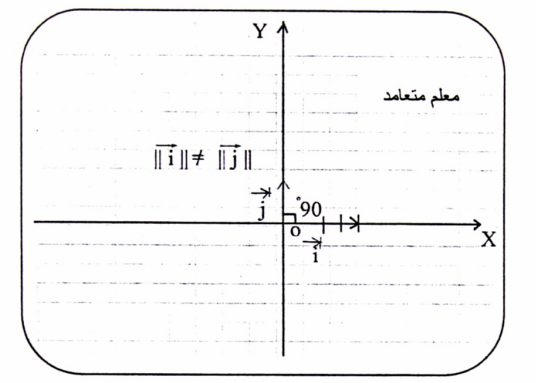
شكل (1-2)
3- معلم متجانس (O , X , Y , I , J) : وهو معلم بسيط للاستخدام في المستوى لتمثيل البيانات. ويختلف عن المعلم المتعامد أن الزاوية بين المحورين ليست 90 درجة ، غير أنه يمتاز بأنه متساوية الطويلة.
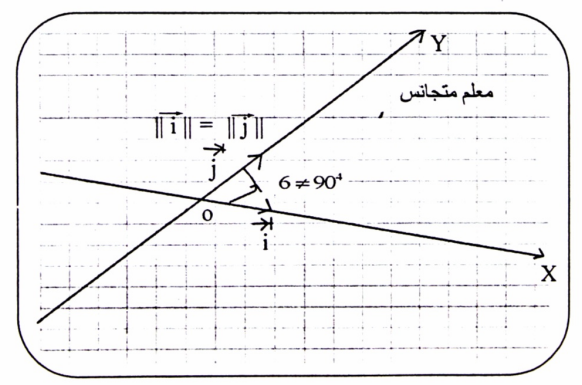
شكل (1-3)
4- معلم متعامد ومتجانس (O , X ,Y , I , J) : وهو معلم أكثر بساطة للاستخدام في المستوى لتمثيل البيانات. ويتميز هذا المعلم بأنه متعامد (أي أن الزاوية بين المحورين ليست 90 درجة) ، وأنه متجانس ( أي أنه متساوي الطويلة).
أي أنه متساوي الطويلة).
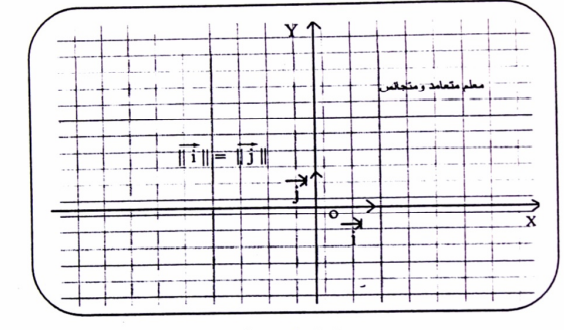
شكل (1-4)
ملاحظة : تفضل استخدام المعلم المتعامد والمتجانس لكل التمثيلات في هذا المقرر، إلا في حالة التعسير ، نستخدم المعلم المتعامد ، وذلك لتوضيح البيانات بنوع من البساطة.
الخطوة الثانية Case Two : نقوم بتشكيل جدول البيانات لنقاط من المجال للمتغير x والتي تقابله من المدى y ، ثم تدوينها في الجدول بالأسلوب الأفقي تارة، أو العمودي تارة أخرى. حسب الوفرة من المساحة ونوع الدالة. والأسلوبان الأفقي والعمودي مشار إليهما في هذين الشكلين :
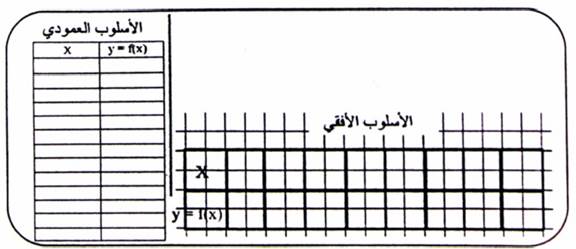
شكل (1-5)
الخطوة الثالثة Case Three : يتم تمثيل ثنائيات (x , y) ، بيانات الجدول المحصل على المستوى المختار ، وليكن المعلم المتعامد والمتجانس.
الخطوة الرابعة Case Four : يتم الربط بين النقاط المحصل عليها خلال المجال بالخط الأملس غير المنكسر ، الذي يعطينا في النهاية المنحنى المطلوب تمثيله.
ملاحظة : يتم توضيح هذه الخطوات الأربع عبر الأمثلة التطبيقية التالية :
مثال (1) : ادرس وارسم منحنى الدالة y = f(x) = x4 في المجال [-1 , 1] .
الحل :
نلاحظ أن مجال الدالة يتكون من ال فترة المستمرة [-1 , 1] ، نحتار بعض النقاط الاساسية وندونها في الجدول الأفقي التالي :

إن تمثيل ثنائيات البيانات المحصل في الجدول تشكل البيان التالي :

شكل (1-6)
مثال (2) : ادرس وارسم منحنى الدالة y = f(x) 4x3 في المجال [-1 , 1].
الحل :
نلاحظ أن مجال الدالة يتكون من الفترة المسترة [-1 , 1] . نختار بعض النقاط الأساسية وندوبها في الجدول الأفقي التالي :

إن تمثيل ثنائيات المحصل في الجدول تشكل البيان التالي:

شكل (1-7)
مثال (3) : ارسم منحنى الدالة y = f(x) = x4 في المجال [0 ,1].
نلاحظ أن مجال الدالة يتكون من الفترة المستمرة [0 ,1]، نختار بعض النقاط الأساسية وندوبها في الجدول الأفقي التالي :

إن تمثيل ثنائيات البيانات المحصل في الجدول تشكل البيان التالي :
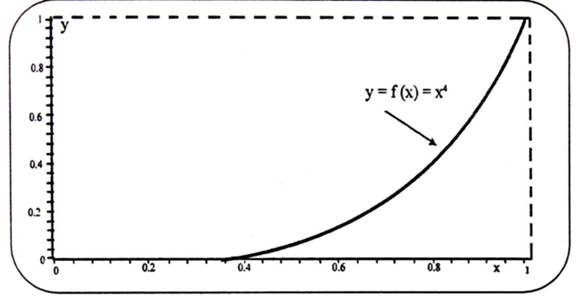
شكل (1-8)
مثال (3) : مثل منحنى الدالة :
F(x) = x2-1
أوجد المستقيم المماس عند الفاصلة x = -3 ؟ .
الحل :
لتوضيح دوال الأسئلة المطروحة سابقاً نقوم بالتمثيل البياني التالي:
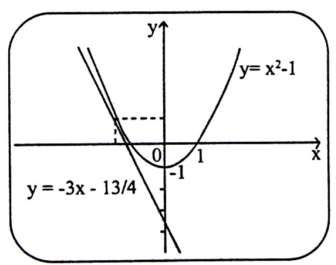
شكل (1-9)
مثال (4) : مثل منحنى الدالة :
Y = f(x) = x3
الحل :
يتضح ان شكل المنحني والذي يمكن ملاحظته بشكل واضح كما هو في الشكل التالي :
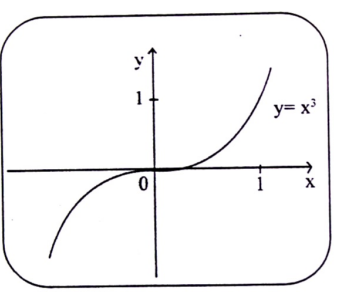
شكل (1-10)
مثال (5) : مثل منحنى الدالة :
g(x) = x1/3
الحل :
يمكن ملاحظة شكل الدالة كما هو في الشكل التالي :
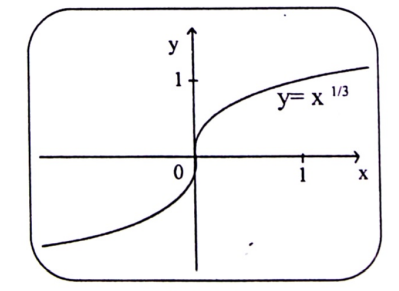
شكل (1-11)
مثال (6) : مثل منحنى الدالة :
F(x) = x4
الحل : يتبين أن منحنى الدالة f(x) = x4 يقبل قيمة حدية صغرى (Iocal minimum) محلية في الفترة [-1 , 1] عند X= 0 ، والشكل هو :
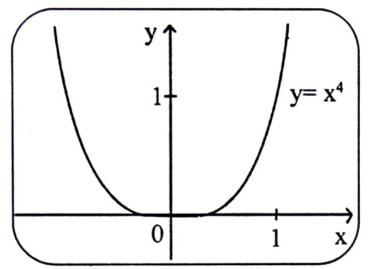
شكل (1-12)
مثال (7) : مثل منحنى الدالة :
F(x) = -x4
الحل :
يتبين أن منحنى الدالة f(x) = -x4 يقبل قيمة حدية عظمى (local maximum) محلية في [-1, 1] عند x = 0 وشكل منحنى الدالة هو :
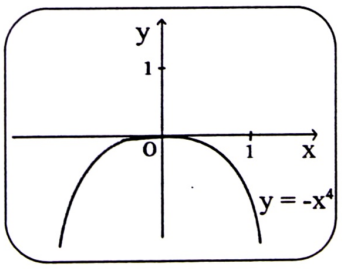
شكل (1-13)
 الاكثر قراءة في التفاضل و التكامل
الاكثر قراءة في التفاضل و التكامل
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















