


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 22-9-2021
Date: 3-10-2021
Date: 12-11-2021
|
The divided difference ![f[x_0,x_1,x_2,...,x_n]](https://mathworld.wolfram.com/images/equations/DividedDifference/Inline1.gif) , sometimes also denoted
, sometimes also denoted ![[x_0,x_1,x_2,...,x_n]](https://mathworld.wolfram.com/images/equations/DividedDifference/Inline2.gif) (Abramowitz and Stegun 1972), on
(Abramowitz and Stegun 1972), on 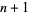 points
points 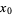 ,
, 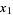 , ...,
, ..., 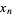 of a function
of a function 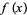 is defined by
is defined by ![f[x_0]=f(x_0)](https://mathworld.wolfram.com/images/equations/DividedDifference/Inline8.gif) and
and
![f[x_0,x_1,...,x_n]=(f[x_0,...,x_(n-1)]-f[x_1,...,x_n])/(x_0-x_n)](https://mathworld.wolfram.com/images/equations/DividedDifference/NumberedEquation1.gif) |
(1) |
for 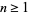 . The first few differences are
. The first few differences are
![f[x_0,x_1]](https://mathworld.wolfram.com/images/equations/DividedDifference/Inline10.gif) |
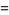 |
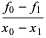 |
(2) |
![f[x_0,x_1,x_2]](https://mathworld.wolfram.com/images/equations/DividedDifference/Inline13.gif) |
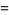 |
![(f[x_0,x_1]-f[x_1,x_2])/(x_0-x_2)](https://mathworld.wolfram.com/images/equations/DividedDifference/Inline15.gif) |
(3) |
![f[x_0,x_1,...,x_n]](https://mathworld.wolfram.com/images/equations/DividedDifference/Inline16.gif) |
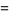 |
![(f[x_0,...,x_(n-1)]-f[x_1,...,x_n])/(x_0-x_n).](https://mathworld.wolfram.com/images/equations/DividedDifference/Inline18.gif) |
(4) |
Defining
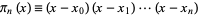 |
(5) |
and taking the derivative
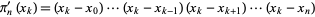 |
(6) |
gives the identity
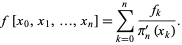 |
(7) |
Consider the following question: does the property
![f[x_1,x_2,...,x_n]=h(x_1+x_2+...+x_n)](https://mathworld.wolfram.com/images/equations/DividedDifference/NumberedEquation5.gif) |
(8) |
for 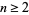 and
and 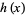 a given function guarantee that
a given function guarantee that 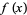 is a polynomial of degree
is a polynomial of degree 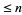 ? Aczél (1985) showed that the answer is "yes" for
? Aczél (1985) showed that the answer is "yes" for 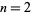 , and Bailey (1992) showed it to be true for
, and Bailey (1992) showed it to be true for 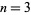 with differentiable
with differentiable 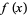 . Schwaiger (1994) and Andersen (1996) subsequently showed the answer to be "yes" for all
. Schwaiger (1994) and Andersen (1996) subsequently showed the answer to be "yes" for all 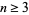 with restrictions on
with restrictions on 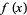 or
or 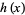 .
.
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 877-878, 1972.
Aczél, J. "A Mean Value Property of the Derivative of Quadratic Polynomials--Without Mean Values and Derivatives." Math. Mag. 58, 42-45, 1985.
Andersen, K. M. "A Characterization of Polynomials." Math. Mag. 69, 137-142, 1996.
Bailey, D. F. "A Mean-Value Property of Cubic Polynomials--Without Mean Values." Math. Mag. 65, 123-124, 1992.
Beyer, W. H. (Ed.). CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, pp. 439-440, 1987.
Jeffreys, H. and Jeffreys, B. S. "Divided Differences." §9.012 in Methods of Mathematical Physics, 3rd ed. Cambridge, England: Cambridge University Press, pp. 260-264, 1988.
Schwaiger, J. "On a Characterization of Polynomials by Divided Differences." Aequationes Math. 48, 317-323, 1994.
Sauer, T. and Xu, Y. "On Multivariate Lagrange Interpolation." Math. Comput. 64, 1147-1170, 1995.
Whittaker, E. T. and Robinson, G. "Divided Differences" and "Theorems on Divided Differences." §11-12 in The Calculus of Observations: A Treatise on Numerical Mathematics, 4th ed. New York: Dover, pp. 20-24, 1967.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
دراسة تستعرض آلام السجناء السياسيين في حقبة البعث المجرم في العراق
|
|
|