


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات Let 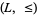 be any complete lattice. Suppose
be any complete lattice. Suppose 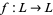 is monotone increasing (or isotone), i.e., for all
is monotone increasing (or isotone), i.e., for all 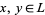 ,
, 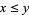 implies
implies 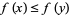 . Then the set of all fixed points of
. Then the set of all fixed points of 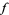 is a complete lattice with respect to
is a complete lattice with respect to 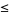 (Tarski 1955)
(Tarski 1955)
Consequently, 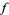 has a greatest fixed point
has a greatest fixed point 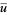 and a least fixed point
and a least fixed point 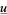 . Moreover, for all
. Moreover, for all 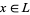 ,
, 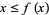 implies
implies 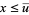 , whereas
, whereas 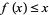 implies
implies 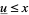 .
.
Consider three examples:
1. Let 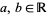 satisfy
satisfy 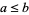 , where
, where 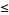 is the usual order of real numbers. Since the closed interval
is the usual order of real numbers. Since the closed interval ![[a,b]](https://mathworld.wolfram.com/images/equations/TarskisFixedPointTheorem/Inline19.gif) is a complete lattice, every monotone increasing map
is a complete lattice, every monotone increasing map ![f:[a,b]->[a,b]](https://mathworld.wolfram.com/images/equations/TarskisFixedPointTheorem/Inline20.gif) has a greatest fixed point and a least fixed point. Note that
has a greatest fixed point and a least fixed point. Note that 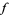 need not be continuous here.
need not be continuous here.
2. For 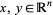 declare
declare 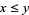 to mean that
to mean that 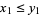 ,
,  ,
, 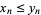 (coordinatewise order). Let
(coordinatewise order). Let 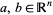 satisfy
satisfy 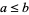 . Then the set
. Then the set
![[a,b]](https://mathworld.wolfram.com/images/equations/TarskisFixedPointTheorem/Inline29.gif) |
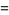 |
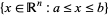 |
(1) |
 |
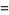 |
![[a_1,b_1]×...×[a_n,b_n]](https://mathworld.wolfram.com/images/equations/TarskisFixedPointTheorem/Inline34.gif) |
(2) |
is a complete lattice (with respect to the coordinatewise order). Hence every monotone increasing map ![f:[a,b]->[a,b]](https://mathworld.wolfram.com/images/equations/TarskisFixedPointTheorem/Inline35.gif) has a greatest fixed point and a least fixed point.
has a greatest fixed point and a least fixed point.
3. Let 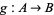 and
and 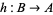 be injections. Then there is a bijection
be injections. Then there is a bijection 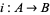 (Schröder-Bernstein theorem), which can be constructed as follows. The power set of
(Schröder-Bernstein theorem), which can be constructed as follows. The power set of 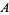 ordered by set inclusion,
ordered by set inclusion, 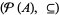 , is a complete lattice. Since the map
, is a complete lattice. Since the map 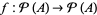 ,
,
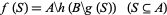 |
(3) |
is monotone increasing, it has a fixed point 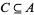 . As
. As 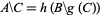 , a bijection
, a bijection 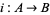 can be defined just by setting
can be defined just by setting
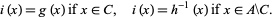 |
(4) |
REFERENCES:
Tarski, A. "A Lattice-Theoretical Fixpoint Theorem and Its Applications." Pacific J. Math. 5, 285-309, 1955.



|
|
|
|
لخفض ضغط الدم.. دراسة تحدد "تمارين مهمة"
|
|
|
|
|
|
|
طال انتظارها.. ميزة جديدة من "واتساب" تعزز الخصوصية
|
|
|
|
|
|
|
عوائل الشهداء: العتبة العباسية المقدسة سبّاقة في استذكار شهداء العراق عبر فعالياتها وأنشطتها المختلفة
|
|
|