


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
أقرأ أيضاً
التاريخ: 29-1-2022
التاريخ: 26-1-2022
التاريخ: 29-1-2022
التاريخ: 26-1-2022
|
الخطوات الأساسية لطريقة السمبلكس
أ- الخطوة الابتدائية: وذلك بإيجاد الحل الابتدائي على النحو التالي:

ب الخطوة الأساسية: إذا افترضنا أن

توقف ويعتبر الحل وهو الحل الأمثل (تصغير) إذا لم يتوفر الشرط المذكور أعلاه اختر الا توقف، فإن الحل هو الأمثل لمساحة غير محدودة خلال الاتجاه.
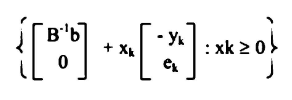
حيث ck مصفوفة الصف الواحد وتحتوي على كل صفر ما عدا عند موقع محدد K. إذا  أحسب الموقع
أحسب الموقع 

واستمر إلى الخطوات التكرارية حتى الحل الأمثل أو غيره.
مثال 6.2
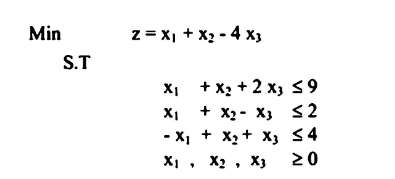
بإضافة (Slack) المتغيرات التي تحصل على إشارة التساوي

وبما أن كل  إذا يمكن اختيار المتغيرات الأساسية التي نبدأ بها الحل
إذا يمكن اختيار المتغيرات الأساسية التي نبدأ بها الحل

محاولة رقم 1
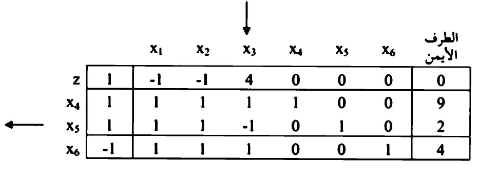
إذا نظرنا إلى الصف صفر (0) نلاحظ وجود قيمة موجبة واحدة مناظرة إلى x3 وبالتالي بقيمة  وهذا يحدد دخول x3 إلى الحل وتصبح من المتغيرات الأساسية لتحسين الوصول إلى الحل الأمثل.
وهذا يحدد دخول x3 إلى الحل وتصبح من المتغيرات الأساسية لتحسين الوصول إلى الحل الأمثل.
ويمكن تحديد (x) التي تخرج من الحل الأساسي من ضمن (x4,x5,x0) وذك باستخدام القاعدة بقسمة العمود (الطرق اليمين) على العمود الذي تم اختياره ونختار أقل قيمة موجبة.

أقل قيمة موجبة هي 4 المقابلة لـ x6
عليه يجب أن تخرج م% وتدخل x وتصبح المحاولة الثانية على الشكل الآتي:

بالنظر إلى الصف 0 مازالت توجد قيمة موجبة (Zj - Cj) مقابلة إلى (3)xj وتطبق نفس الخطوات للمحاولة الثالثة.
المحاولة الثالثة:

وبما أن كل  لجميع المتغيرات غير الأساسية.
لجميع المتغيرات غير الأساسية.
الحل هو الأمثل وقيم الحل هي:
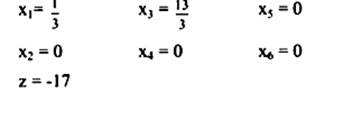



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
عقد جلسة حوارية عن ضحايا جرائم التطرف ضمن فعاليات اليوم الثاني لمؤتمر ذاكرة الألم
|
|
|