


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
أقرأ أيضاً
التاريخ: 15-3-2016
التاريخ: 29-2-2016
التاريخ: 14-3-2016
التاريخ: 20-3-2016
|
المصفوفة هي ترتيب مستطيل الشكل من الأعداد الحقيقية. الأعداد في هذا الترتيب تسمى عناصر المصفوفة.
مثال(1):
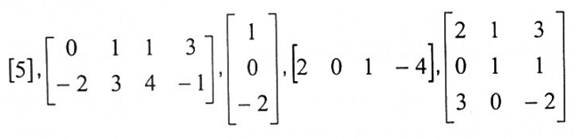
هذه الأشكال تسمى مصفوفات.
الخطوط الأفقية للعناصر تسمى صفوفاً والخطوط العمودية تسمى أعمدة.
عدد الصفوف (الخطوط الأفقية) وعدد الأعمدة (الخطوط العمودية) يسمى سعة المصفوفة. فمثلاً المصفوفة الأولى تحتوي على ثلاثة مصفوفات وثلاث أعمدة لذا فسعتها 3x3. اما المصفوفة الأولى تحتوي على صف واحد وأربع أعمدة فسعتها ، إذن 1x4، اما بقية المصفوفات فسعتها: 3 x 1 , 2 x 4 , 1 x 1 على التوالي. تستخدم الحروف الكبيرة A , B , ... لتسمية المصفوفات والعنصر الواقع في الصف رقم i والعمود رقم j يرمز له بالرمز aij.
وبشكل عام المصفوفة التي سعتها mxn تكتب بالشكل:

عندما يكون عدد الصفوف مساوياً لعدد الأعمدة فإن A تسمى مصفوفة مربعة سعتها n x n قطر المصفوفة المربعة الذي عناصره a11 , a22 , … ann يسمى القطر الرئيسي كما موضح أدناه:
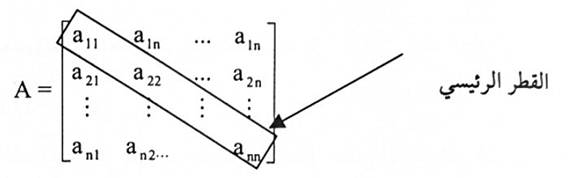
العمليات على المصفوفة:
يقال للمصفوفتين B , A بأنهما متساويتين إذا تساوت سعتهما والعناصر المتقابلة فيهما.
إذا كانت [aij] , A = [bij] B = فإن A = B إذا وفقط إذا aij = bij لكل j , i حيث I,j = 1, 2, … , n
تعريف (1-1):
إذا كانj B,A مصفوفتين بنفس السعة فإن جميعها A + B هو مصفوفة C يمكن الحصول عليها بإضافة عناصر المصفوفة A إلى عناصر B المتناظرة.
ملاحظة:
إذا كانت سعة A تختلف عن سعة B فإن جميعها A + B يكون غير معرف.
مثال (2):
لتكن
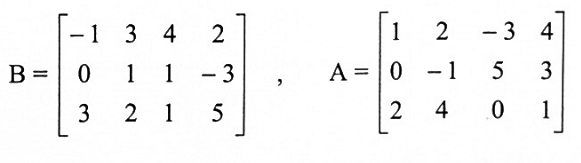
 ملاحظة:
ملاحظة:
طرح المصفوفات هي حالة خاصة لعملية الجمع والضرب بكمية ثابتة -1.
فمثلاً إذا كانت A و B مصفوفتان كما في المثال (2) فإن:
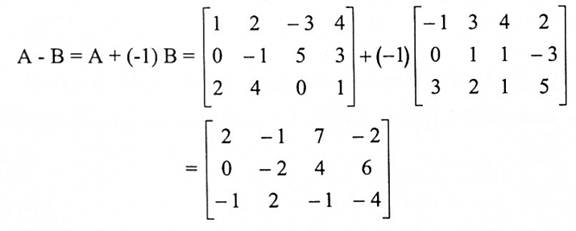
تعريف (1-2):
لتكن] A=[aij مصفوفة و k كمية ثابتة فإن ضربهما KA هو المصفوفة الناتجة من ضرب كل عنصر في A بالكمية الثابتة k، أي أن:
KA=[Kaij]
مثال (3):

تعريف (1-3):
لتكن A = [aij] سعتها m x n , [bij] و B سعتها p x q فإن ضربهما، C = AB هو مصفوفة، شريطة أن يكون عدد أعمدة A مساوياً لعدد صفوف B أي أن n = p ويكون حاصل الضرب هو:
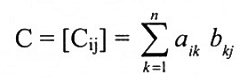
التي سعتها m x q
للحصول على العناصر Cij في C نضرب عناصر الصف في الموقع i من المصفوفة A بالعناصر المقابلة في العمود رقم j من المصفوفة B ثم نجمع حواصل الضرب.
مثال (4):
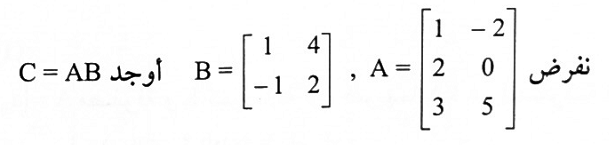
الحل:
بما أن عدد اعمدة A يساوي عدد صفوف B فإن الضرب AB يكون معرفاً.
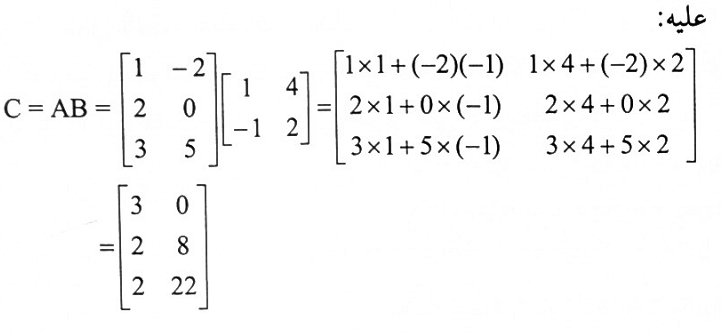
ملاحظة:
عملية الضرب BA في المثال (4) غير معرفة لأن عدد أعمدة B لا يساوي عدد صفوف A.
وبصورة عامة إذا كانت [aij] A = سعتها mxr و [bij]B = سعتها r x n فإن العنصر Cij هو:
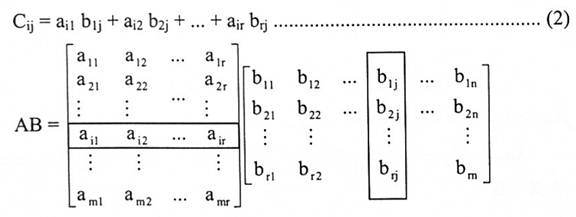
الشكل المصفوفي لأنظمة المعادلات الخطية:
لضرب المصفوفات تطبيقات مهمة في أنظمة المعادلات الخطية. خذ أي نظام متكون من m من المعادلات الخطية التي تحتوي على n من المتغيرات:

وإذا اسمينا مصفوفة المعاملات بالرمز A ومصفوفة المتغيرات بالرمز x ومصفوفة الثوابت بالرمز B، فإن النظام أعلاه يمكن كتابته بالصيغة المبسطة:
A X = B
ضرب المصفوفات كتركيب خطي:
تزودنا مصفوفات والأعمدة بأفكار بديلة لضرب المصفوفات، فمثلاً افترض أن:

فإن
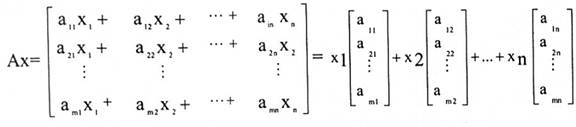
أي أن AX هي تركيب خطي لأعمدة A مركباتها من المصفوفة x.
مثال (5):

تعريف (1-4):
إذا كانت A مصفوفة سعتها m x n فإن منقوله A، تكتب AT ، وتعرف بأنها المصفوفة الناتجة من تبديل صفوف A بأعمدتها وتكون سعتها n x m
ملاحظة:
العمود الأول في AT هو الصف الأول في A والعمود الثاني في AT هو الصف الثاني في A وهكذا.
مثال (6):
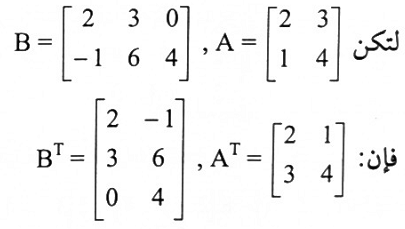
تعريف (1-5):
إذا كانت A مصفوفة مربعة فإن أثر A (يكتب (A) tr) يعرف بأنه مجموع العناصر الواقعة في القطر الرئيسي.
مثال (7):
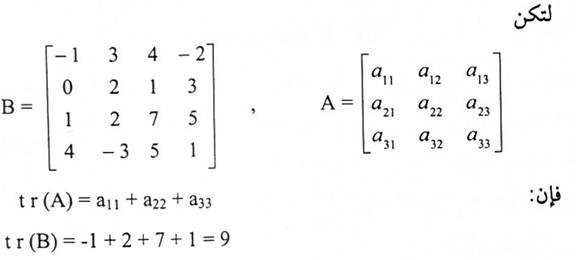



|
|
|
|
دراسة تحدد أفضل 4 وجبات صحية.. وأخطرها
|
|
|
|
|
|
|
العتبة العباسية تحتفي بذكرى ولادة الإمام الجواد (عليه السلام) في مشاتل الكفيل
|
|
|