
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
الخواص البصرية للبلورات
المؤلف:
أ.د. نعيمة عبد القادر أحمد / أ.د. محمد أمين سلمان
المصدر:
علم البلورات والاشعة السينية
الجزء والصفحة:
ص82–85
2023-09-19
1467
يختلف سلوك البلورات عند مرور الضوء من خلالها تبعا لتماثلها. ومن أهم الظواهر المرتبطة بهذا السلوك ظاهرة الانكسار المزدوج Birefringence. وقد يكون هذا الانكسار المزدوج طبيعيا نتيجة كون البلورة لا أيزوتروبية بطبعها، أو اصطناعيا نتيجة تطبيق مجال خارجي على البلورة. فالمجال الكهربائي يؤدي إلى الظاهرة الكهروبصرية، أما المجال المغناطيسي فيؤدي إلى حدوث ظاهرة فاراداي. وتتمتع بعض البلورات بخواص بصرية أخرى كالنشاط البصرى، حيث تقوم البلورة بإدارة مستوى استقطاب الضوء المار خلالها.
وقد اعتبر المجسم الممثل لغير معاملات الانكسار مع الاتجاهات أساسا لتصنيف البلورات من حيث خواصها البصرية كما يلي:
أ - الأجسام الايزوتروبية – موحدة الخواص
تتحدد الخواص العزلية في الأجسام الأيزوتروبية عند الترددات العالية بالعلاقات:
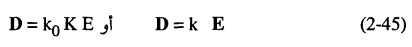
حيث k سماحية الجسم و k0 سماحية الفراغ، K هو ثابت العازل، وإذا اعتبرنا أن النفاذية المغناطيسية النسبية تساوي الوحدة فإن معادلات ماكسويل تؤول إلى أن سرعة انتشار الموجات الكهرومغناطيسية خلال الوسط هي:

حيث c هي سرعة تلك الموجات في الفراغ، أما معامل الانكسار n فهو:

ب - الأجسام اللاايزوتروبية – غير موحدة الخواص
إذا رجعنا إلى المعادلتين (37-2)، (38-2) فإننا ندرك على الفور أن العلاقة يجب أن تستبدل بها العلاقة الآتية في حالة الأجسام اللاأيزوتروبية:

ونعلم من مقرر البصريات الفيزيائية أن موجات الضوء تنقسم داخل البلورة اللاأيزوتروبية إلى نوعين من الموجات ولكل منها سرعة خاصة به، كما أن كلا النوعين مستقطبا استوائيا. وتسمى النسبة c/v = n لكل موجة معامل إنكسار تلك الموجة. ويمكن تمثيل معاملات إنكسار الموجتين والعمود الموجي المشترك لهما بمجسم قطع ناقص ولو كانت المحاور 1x، 2x، x3 هي المحاور الرئيسية لممتد ثابت العازل (أو السماحية) فإن معادلة المجسم تكون:

ويبين الشكل (2-8) المجسم المذكور أعلاه والذي يتمتع بالخاصية الآتية:
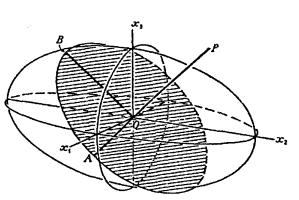
شكل (8-2)
مجسم معاملات الانكسار الذي يعطى قيم معاملي الانكسار واتجاهات تذبذب D للموجتين المستقطبتين استوائيا
هب أننا رسمنا خطا مستقيما OP يمر بنقطة الأصل وفي أي اتجاه، ثم لنتخيل مقطعا مركزيا متعامدا مع ذلك الخط. ولا بد أن يكون هذا المقطع قطعا ناقصا. تنتشر جبهتان موجيتان عموديا على OP خلال البلورة، ويكون معاملا انكسارهما مساويين لأنصاف محاور ذلك القطع الناقص وهما OA وOB. أما متجه الإزاحة الكهربائية D فيتذبذب في الموجة المستقطبة استوائيا والتي معامل انكسارها OA بحيث يكون موازيا للخط OA.
وبالمثل يتذبذب متجه الإزاحة في الموجة التي معامل انكسارها يساوى OB بحيث يكون موازيا للخط OB. وتسمى n1،n2 ، n3 معاملات الانكسار الرئيسية جدير بالملاحظة أن معاملات الانكسار نفسها ليست كميات ممتدة على الرغم من أن تغيرها مع الاتجاهات يتحدد كما رأينا من ثابت العزل الذي هو كمية ممتدة.
ولا بد أن ينعكس تماثل البلورة على مجسم معاملات الانكسار حيث يكون المجسم الخاص ببلورة مكعبية على هيئة كرة. وبديهي أن كل مقاطع الكرة المركزية هي دوائر ولذلك تظهر مثل هذه البلورات انكسارا مزدوجا.
أما في حالة البلورات السداسية والرباعية والثلاثية فإن المجسم لا بد وأن يتخذ شكل مجسم قطع ناقص Ellipsoid دوراني حول محور التماثل الرئيسي (الشكل 2-9)؛ فإذا كان هذا المحور هو x3 فإن المعادلة تصبح:
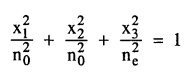
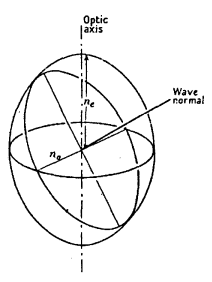
شكل (2-9)
مجسم معاملات الانكسار لا لبلورة أحادية المحور (موجبة)
وهناك مقطع واحد متعامد المحور الرئيسي وهو على شكل دائرة نصف قطرها n0، ومن ثم لا يظهر به انكسار مزدوج عندما يكون العمود الموجي في اتجاه المحور الرئيسي، الذي يسمى في هذه الحالة المحور البصري.
ويطلق على هذه البلورات مصطلح أحادية المحور، كما يسمى n0 معامل الانكسار الاعتيادي ne معامل الانكسار غير الاعتيادي وإذا كان (ne – n0) موجبا وصفت البلورة بأنها موجبة أما إذا كان سالبا فالبلورة سالبة.
بقيت مجموعات بلورية ثلاث هي المعينية القائمة وأحادية الميل وثلاثية الميل، وهذه يمكن تمثيلها بمجسم قطع ناقص ثلاثي المحاور يتمتع بمقطعين دائريين (الشكل 2-10)؛ ولذلك يكون هناك اتجاهان مفضلان للعمود الموجي لا يحدث في اتجاههما انكسار مزدوج وهذان الاتجاهان هما المحوران البصريان الأوليان أو ببساطة المحوران البصريان ... أما البلورة فتكون ثنائية المحور.
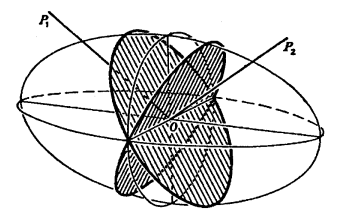
شكل (2-10)
يوضح الشكل المقطعين الدائريين والمحورين البصريين OP2, OP1 لبلورة ثنائية المحور
 الاكثر قراءة في مواضيع عامة في الفيزياء الصلبة
الاكثر قراءة في مواضيع عامة في الفيزياء الصلبة
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















