


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
أقرأ أيضاً
التاريخ: 13-12-2020
التاريخ: 2023-05-21
التاريخ: 2023-05-06
التاريخ: 2023-04-16
|
Now, what about the second law of thermodynamics? We know that if we do work against friction, say, the work lost to us is equal to the heat produced. If we do work in a room at temperature T, and we do the work slowly enough, the room temperature does not change much, and we have converted work into heat at a given temperature. What about the reverse possibility? Is it possible to convert the heat back into work at a given temperature? The second law of thermodynamics asserts that it is not. It would be very convenient to be able to convert heat into work merely by reversing a process like friction. If we consider only the conservation of energy, we might think that heat energy, such as that in the vibrational motions of molecules, might provide a goodly supply of useful energy. But Carnot assumed that it is impossible to extract the energy of heat at a single temperature. In other words, if the whole world were at the same temperature, one could not convert any of its heat energy into work: while the process of making work go into heat can take place at a given temperature, one cannot reverse it to get the work back again. Specifically, Carnot assumed that heat cannot be taken in at a certain temperature and converted into work with no other change in the system or the surroundings.
That last phrase is very important. Suppose we have a can of compressed air at a certain temperature, and we let the air expand. It can do work; it can make hammers go, for example. It cools off a little in the expansion, but if we had a big sea, like the ocean, at a given temperature—a heat reservoir—we could warm it up again. So we have taken the heat out of the sea, and we have done work with the compressed air. But Carnot was not wrong, because we did not leave everything as it was. If we recompress the air that we let expand, we will find we are doing extra work, and when we are finished we will discover that we not only got no work out of the system at temperature T, but we actually put some in. We must talk only about situations in which the net result of the whole process is to take heat away and convert it into work, just as the net result of the process of doing work against friction is to take work and convert it into heat. If we move in a circle, we can bring the system back precisely to its starting point, with the net result that we did work against friction and produced heat. Can we reverse the process? Turn a switch, so that everything goes backwards, so the friction does work against us, and cools the sea? According to Carnot: no! So let us suppose that this is impossible.
If it were possible it would mean, among other things, that we could take heat out of a cold body and put it into a hot body at no cost, as it were. Now we know it is natural that a hot thing can warm up a cool thing; if we simply put a hot body and a cold one together, and change nothing else, our experience assures us that it is not going to happen that the hot one gets hotter, and the cold one gets colder! But if we could obtain work by extracting the heat out of the ocean, say, or from anything else at a single temperature, then that work could be converted back into heat by friction at some other temperature. For instance, the other arm of a working machine could be rubbing something that is already hot. The net result would be to take heat from a “cold” body, the ocean, and to put it into a hot body. Now, the hypothesis of Carnot, the second law of thermodynamics, is sometimes stated as follows: heat cannot, of itself, flow from a cold to a hot object. But, as we have just seen, these two statements are equivalent: first, that one cannot devise a process whose only result is to convert heat to work at a single temperature, and second, that one cannot make heat flow by itself from a cold to a hot place. We shall mostly use the first form.
Carnot’s analysis of heat engines is quite similar to the argument that we gave about weight-lifting engines in our discussion of the conservation of energy in Chapter 4. In fact, that argument was patterned after Carnot’s argument about heat engines, and so the present treatment will sound very much the same.
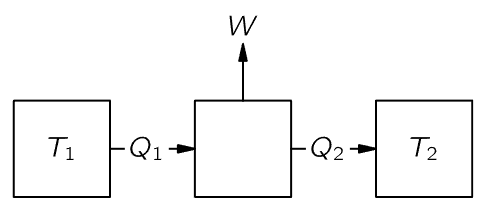
Fig. 44–3. Heat engine.
Suppose we build a heat engine that has a “boiler” somewhere at a temperature T1. A certain heat Q1 is taken from the boiler, the steam engine does some work W, and it then delivers some heat Q2 into a “condenser” at another temperature T2 (Fig. 44–3). Carnot did not say how much heat, because he did not know the first law, and he did not use the law that Q2 was equal to Q1 because he did not believe it. Although everybody thought that, according to the caloric theory, the heats Q1 and Q2 would have to be the same, Carnot did not say they were the same—that is part of the cleverness of his argument. If we do use the first law, we find that the heat delivered, Q2, is the heat Q1 that was put in minus the work W that was done:
Q2=Q1−W. (44.3)
(If we have some kind of cyclic process where water is pumped back into the boiler after it is condensed, we will say that we have heat Q1 absorbed and work W done, during each cycle, for a certain amount of water that goes around the cycle.)
Now we shall build another engine, and see if we cannot get more work from the same amount of heat being delivered at the temperature T1, with the condenser still at the temperature T2. We shall use the same amount of heat Q1 from the boiler, and we shall try to get more work than we did out of the steam engine, perhaps by using another fluid, such as alcohol.



|
|
|
|
لشعر لامع وكثيف وصحي.. وصفة تكشف "سرا آسيويا" قديما
|
|
|
|
|
|
|
كيفية الحفاظ على فرامل السيارة لضمان الأمان المثالي
|
|
|
|
|
|
|
قسم التربية والتعليم يطلق الامتحانات النهائية لمتعلِّمات مجموعة العميد التربوية للبنات
|
|
|