

Grammar


Tenses


Present

Present Simple

Present Continuous

Present Perfect

Present Perfect Continuous


Past

Past Simple

Past Continuous

Past Perfect

Past Perfect Continuous


Future

Future Simple

Future Continuous

Future Perfect

Future Perfect Continuous


Parts Of Speech


Nouns

Countable and uncountable nouns

Verbal nouns

Singular and Plural nouns

Proper nouns

Nouns gender

Nouns definition

Concrete nouns

Abstract nouns

Common nouns

Collective nouns

Definition Of Nouns

Animate and Inanimate nouns

Nouns


Verbs

Stative and dynamic verbs

Finite and nonfinite verbs

To be verbs

Transitive and intransitive verbs

Auxiliary verbs

Modal verbs

Regular and irregular verbs

Action verbs

Verbs


Adverbs

Relative adverbs

Interrogative adverbs

Adverbs of time

Adverbs of place

Adverbs of reason

Adverbs of quantity

Adverbs of manner

Adverbs of frequency

Adverbs of affirmation

Adverbs


Adjectives

Quantitative adjective

Proper adjective

Possessive adjective

Numeral adjective

Interrogative adjective

Distributive adjective

Descriptive adjective

Demonstrative adjective


Pronouns

Subject pronoun

Relative pronoun

Reflexive pronoun

Reciprocal pronoun

Possessive pronoun

Personal pronoun

Interrogative pronoun

Indefinite pronoun

Emphatic pronoun

Distributive pronoun

Demonstrative pronoun

Pronouns


Pre Position


Preposition by function

Time preposition

Reason preposition

Possession preposition

Place preposition

Phrases preposition

Origin preposition

Measure preposition

Direction preposition

Contrast preposition

Agent preposition


Preposition by construction

Simple preposition

Phrase preposition

Double preposition

Compound preposition

prepositions


Conjunctions

Subordinating conjunction

Correlative conjunction

Coordinating conjunction

Conjunctive adverbs

conjunctions


Interjections

Express calling interjection

Phrases

Sentences


Grammar Rules

Passive and Active

Preference

Requests and offers

wishes

Be used to

Some and any

Could have done

Describing people

Giving advices

Possession

Comparative and superlative

Giving Reason

Making Suggestions

Apologizing

Forming questions

Since and for

Directions

Obligation

Adverbials

invitation

Articles

Imaginary condition

Zero conditional

First conditional

Second conditional

Third conditional

Reported speech

Demonstratives

Determiners


Linguistics

Phonetics

Phonology

Linguistics fields

Syntax

Morphology

Semantics

pragmatics

History

Writing

Grammar

Phonetics and Phonology

Semiotics


Reading Comprehension

Elementary

Intermediate

Advanced


Teaching Methods

Teaching Strategies

Assessment
Some problems of primary arguments
المؤلف:
MANFRED BIERWISCH
المصدر:
Semantics AN INTERDISCIPLINARY READER IN PHILOSOPHY, LINGUISTICS AND PSYCHOLOGY
الجزء والصفحة:
413-24
2024-08-16
1049
Some problems of primary arguments
Before pursuing further the classification of semantic features, it may be expedient to consider in somewhat greater detail the interpretation of the variables Xi just introduced, since a perhaps fundamental divergence from the status of variables used in the predicate calculus is necessary. The problems involved are rather complicated: I cannot even list them completely, to say nothing of an adequate solution.
First of all syntactic reference indices indicate reference instances which by no means always consist exactly of one individual as in the examples (ɪ)-(4). They may comprise finite and even infinite sets of individuals as well:
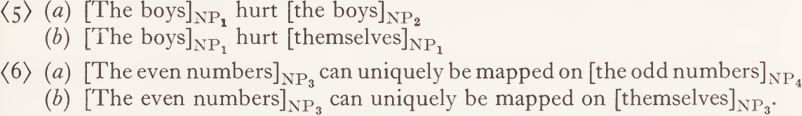
Thus reference indices in general correspond to sets of individuals, including sets containing one element.
Secondly, two or more sets reflected by respective reference indices can be joined to form a new reference instance:

Notice that sentences of this type cannot be derived from a conjunction of underlying sentences without conjoined NPs. The index 4 of the possessive NP ‘their’ obviously joins together the indices 1, 2, and 3, just as these and the index 5 are covered by the index 6.
On the other hand, reference instances may be split up into several particular instances represented by particular indices:
(8) [The teachers] NP1 disagreed about the proposal2 since [the younger ones] NP3 were optimistic whereas [the others]NP4 were not.
In this example the instance 1 is divided into the separate instances 3 and 4. More complicated cases can easily be found.
Observations of this kind suggest the introduction of certain set theoretical operations over reference indices, and hence also over the corresponding variables occurring in the semantic interpretations.1 It seems to me that set theoretical sum and difference are necessary and probably sufficient. They may be defined in the following way:
(9) Let i, j, k be reference indices, Xi Xj, Kk the corresponding variables, and a1,a2,. . .,an,b1,b2,. . .,bm  variables for single objects to be referred to. Then
variables for single objects to be referred to. Then
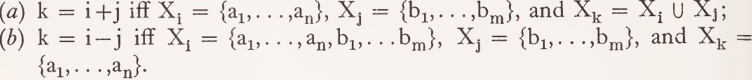
Notice that even the a1 through bm are not representations of particular (real or fictitious) objects, but variables for such objects, since we are still concerned with identity and difference of reference, not with reference itself. With this definition in mind, we can replace (7) and (8) by (10) and (11) respectively:
(10) [John1, Paul2, Bill3, and [their 1+2+3 wives]Np5]NP1+2+3+5 squeezed [them-selves] NP1+2+3+5 into [one little car]Np7.
(11) [The teachers] NP1 disagreed about the proposal2 since [the younger ones] NP (1-r) were optimistic whereas [the others]NP 1- (1-r)were not.
The index 1-r in (11) contains a variable r which does not specify a reference instance in itself, but serves only to divide the set represented by 1. This represents the fact that the instance 3 = 1-r is constructed from instance 1, and 4 = 1 —(1-r) from 1 and 3 in the obvious way.2
Notice that the variable X1+2+3+5 corresponding to the index of the node dominating the whole subject-NP in (10) need not appear within the reading of this NP itself. This reading contains rather the variables X1, X2, X3, X5, and X1+2+3 corresponding to the respective constituent NPs. But the variable X1+2+3+5 will be substituted for the subject variable of the verb.
Turning now to the semantic aspect of the reference indices and the variables corresponding to them, the following interpretation might seem plausible. If P is a semantic feature (or a complex of features) and Xi its argument, then P is predicated of every element contained in Xi More formally: 3
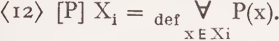
Although this interpretation covers a certain class of cases, it cannot be accepted in general. We will briefly discuss some classes of counterexamples.
Difficulties arise already in such simple cases as (13):
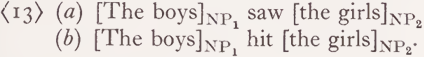
Ignoring all details not relevant for the present discussion, and using ‘B’, ‘G’, ‘S’, and ‘H’ as abbreviations for the complexes of semantic features of the readings of ‘boy’, ‘girl’, ‘saw’, and ‘hit’, respectively, the readings of (13 a) and (13 b) can be given roughly as (14 a) and (14 b):
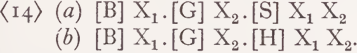
Applying definition (12) we arrive at the representations (15 a) and (15 b):
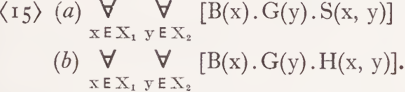
Whereas (15 a) gives a fairly correct account of the way in which (13 a) is understood, this does not hold with respect to (15 b) and (13 b), since (13 b) does not assert that every single boy thrashed every single girl. One might try to remedy this failure within the framework of the predicate calculus, e.g. by introducing a second convention for the interpretation of variables corresponding to reference indices to the effect that the universal quantifier is replaced under certain conditions by the existential quantifier, thereby rendering (15 b) into (16):

Although this doubtless corresponds more closely to the way in which (13 b) is understood, it does not work. (16) does not claim, to be sure, that every boy hit every girl, but it fails to express that, at least in principle, every girl from the group X2 is thrashed by at least one boy, as implied by (13 b). Moreover, any attempt to get along with universal and existential quantifiers will be dependent much too strongly on idiosyncratic properties of the dictionary entries involved. And in many cases it forces completely unmotivated decisions. Consider sentences such as ‘The boys loved the girls’, ‘The boys chased the girls’, etc.
A still more serious obstacle is hidden in sentences like (7), where the reading of ‘squeeze’ cannot be distributed separately on the individuals contained in the reference instance X6 = X1+2+3+5. The squeezing is understood obviously as an action brought about by the group as a whole. This is still more obvious in sentences like:

The problem involved here is connected with what McCawley (1968) has tried to explain by the feature ‘Joint’. In cases of jointness the predication does not apply separately to the individuals referred to.4
A related, but still different problem arises in sentences like:
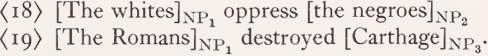
Like (7) and (17) these examples do not apply to the elements of the relevant reference instances individually. But beyond this it is understood that not all individuals comprised under NP1 and NP2 of (18) and (19) are in fact involved in the relevant actions or relations. Rather the groups referred to are understood as a plurality whose individuals are not singled out with respect to participation or nonparticipation in the states and processes in question. It is claimed only that the group as a whole is concerned. Notice that such considerations apply also to apparently trivial cases of non-joint verbs like ‘ know ’:
(20) [The Chinese of the seventh century]NP1 knew porcelain.
By uttering (20) one does not claim that everybody in the China of the seventh century had the relevant knowledge. (20) is true also under the weaker condition that the Chinese people as a whole knew porcelain.
From these and similar considerations I conclude that an interpretation of reference indices and corresponding arguments along the lines indicated by (12) must be given up. Instead of this I propose to consider an argument Xi as a variable to be substituted by the representation of a fraction of the (real or fictitious) universe talked about. This fraction is made up from one or more equivalent objects or individuals which are singled out for separate predication only under specific conditions. These conditions are either part of the predicates to be applied or expressed by particular specifiers and quantifiers such as ‘every’, ‘all’, ‘two’, ‘many’, etc. Further factors may possibly be involved. This proposal would account in a natural way for the ‘ indeterminacy ’ of the distribution of the relevant predicates on the particular individuals in cases like (13) and (17)-(2o), where no individualizing features are involved. I do not try to formalize this proposal concerning the interpretation of reference instances, since any serious formal account of these problems would have to deal with many problems which are too poorly understood at present. I suspect however that the proposed concept of ‘ global reference ’ cannot be explained in terms of more basic notions of a semantic theory, but must be taken as a primitive notion itself. I presume, in other words, that in this respect the quantification theory of modern logic and the linguistic semantic theory are radically different in that they take the inverse direction: whereas quantification theory takes individuals as the starting point from which exhaustive and partial sets are constructed by means of universal and existential quantification, linguistic semantics probably has to start with sets as primitive terms which may further be specified with respect to the participation of their elements in particular state of affairs. This means, that what is a particular case in linguistic semantics has been taken as the basic one within the quantification theory according to the special purpose of its construction. But these are vague speculations which must be motivated much more carefully.
1 Notice that the availability of such operations is necessary for purely syntactic reasons. To give only a simple example, how could we account in a non-ad-hoc manner for the following facts without knowing that index 3 is made up from 1 and 2?
(i) John1 squeezed Bill2 and himself1 into a car4.
(ii) *John1 and Bill2 squeezed himself1 and himself2 into a car4.
(iii) [John1 and Bill2]NP3 squeezed themselves3 into a car4.
Similar operations on reference indices are involved in the following examples:

Such and still more complicated phenomena of pronominalization and deletion have been little explored until now. They obviously require a certain algebra of reference indices.
2 Similar assumptions with respect to set theoretical operations on reference indices have been made by McCawley (1968). There is only a slight difference. McCawley considers sets of one element as individuals, not as sets. He allows them, however, to be subject to set theoretical operations. I do not see any reason for this peculiarity. McCawley claims that one of the conditions for the choice of number affixes in NPs is the decision as to whether their reference index is a set or an individual. But a rule that can distinguish between a set index and an individual index might be sensible as well for the distinction between sets containing one element and sets containing more then one element. - There are some doubts, by the way, with respect to McCawley’s assumption that sets of two or more elements are converted into grammatical plural morphemes. See pp. 430-1, note c for a counterexample.
3 I use the notation ‘ [P] X1 X2. . .Xk’ for a k-place predicate assigned to its k arguments. For some motivation of this notation see Bierwisch (1969).
4 The shortcomings of McCawley’s analysis of this problem and the different aspects of jointness have been discussed carefully by Lang (1967). I cannot go into the details here.
 الاكثر قراءة في Semantics
الاكثر قراءة في Semantics
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















