

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Bayes,s theory
المؤلف:
Tony Crilly
المصدر:
50 mathematical ideas you really need to know
الجزء والصفحة:
187-191
20-2-2016
1823
The early years of the Rev. Thomas Bayes are obscure. Born in the southeast of England, probably in 1702, he became a nonconformist minister of religion, but also gained a reputation as a mathematician and was elected to the Royal Society of London in 1742. Bayes’s famous Essay towards solving a problem in the doctrine of chances was published in 1763, two years after his death. It gave a formula for finding inverse probability, the probability ‘the other way around’, and it helped create a concept central to Bayesian philosophy – conditional probability.
Thomas Bayes has given his name to the Bayesians, the adherents of a brand of statistics at variance with traditional statisticians or ‘frequentists’. The frequentists adopt a view of probability based on hard numerical data. Bayesian views are centred on the famous Bayes’s formula and the principle that subjective degrees of belief can be treated as mathematical probability.
Conditional probability
Imagine that the dashing Dr Why has the task of diagnosing measles in his patients. The appearance of spots is an indicator used for detection but diagnosis is not straightforward. A patient may have measles without having spots and some patients may have spots without having measles. The probability that a patient has spots given that they have measles is a conditional probability. Bayesians use a vertical line in their formulae to mean ‘given’, so if we write
prob(a patient has spots | the patient has measles)
it means the probability that a patient has spots given that they have measles. The value of prob(a patient has spots|the patient has measles) is not the same as prob(the patient has measles|the patient has spots). In relation to each other, one is the probability the other way around. Bayes’s formula is the formula of calculating one from the other. Mathematicians like nothing better than using notation to stand for things. So let’s say the event of having measles is M and the event of a patient having spots is S. The symbol is the event of a patient not having spots and  the event of not having measles. We can see this on a Venn diagram.
the event of not having measles. We can see this on a Venn diagram.
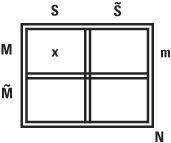
Venn diagram showing the logical structure of the appearance of spots and measles
This tells Dr Why that there are x patients who have measles and spots, m patients who have measles, while the total number of patients overall is N. From the diagram he can see that the probability that someone has measles and has spots is simply x/N, while the probability that someone has measles is m/N. The conditional probability, the probability that someone has spots given that they have measles, written prob(S|M), is x/m. Putting these together, Dr Why gets the probability that someone has both measles and spots
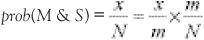
or
prob(M & S) = prob(S|M) × prob(M)
and similarly
prob(M & S) = prob(M|S) × prob(S)

Bayes’s formula
Bayes’s formula
Equating the expressions for prob(M & S) gives Bayes’s formula, the relationship between the conditional probability and its inverse. Dr Why will have a good idea about prob(S|M), the probability that if a patient has measles, they have spots. The conditional probability the other way around is what Dr Why is really interested in, his estimate of whether a patient has measles if they present with spots. Finding this out is the inverse problem and the kind of problem addressed by Bayes in his essay. To work out the probabilities we need to put in some numbers. These will be subjective but what is important is to see how they combine. The probability that if patients have measles, they have spots, prob(S|M) will be high, say 0.9 and if the patient does not have measles, the probability of them having spots prob(S|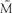 ) will be low, say 0.15. In both these situations Dr Why will have a good idea of the values of these probabilities. The dashing doctor will also have an idea about the percentage of people in the population who have measles, say 20%. This is expressed as prob(M) = 0.2. The only other piece of information we need is prob(S), the percentage of people in the population who have spots. Now the probability of someone having spots is the probability of someone having measles and spots plus the probability that someone does not have measles but does have spots. From our key relations, prob(S) = 0.9 × 0.2 + 0.15 × 0.8 = 0.3. Substituting these values into Bayes’s formula gives:
) will be low, say 0.15. In both these situations Dr Why will have a good idea of the values of these probabilities. The dashing doctor will also have an idea about the percentage of people in the population who have measles, say 20%. This is expressed as prob(M) = 0.2. The only other piece of information we need is prob(S), the percentage of people in the population who have spots. Now the probability of someone having spots is the probability of someone having measles and spots plus the probability that someone does not have measles but does have spots. From our key relations, prob(S) = 0.9 × 0.2 + 0.15 × 0.8 = 0.3. Substituting these values into Bayes’s formula gives:
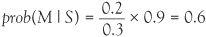
The conclusion is that from all the patients with spots that the doctor sees he correctly detects measles in 60% of his cases. Suppose now that the doctor receives more information on the strain of measles so that the probability of detection goes up, that is prob(S|M) the probability of having spots from measles, increases from 0.9 to 0.95 and prob(S| ), the probability of spots from some other cause, declines from 0.15 to 0.1. How does this change improve his rate of measles detection? What is the new prob(M|S)? With this new information, prob(S) = 0.95 × 0.2 + 0.1 × 0.8 = 0.27, so in Bayes’s formula, prob(M|S) is 0.2 divided by prob(S) = 0.27 and then all multiplied by 0.95, which comes to 0.704. So Dr Why can now detect 70% of cases with this improved information. If the probabilities changed to 0.99, and 0.01 respectively then the detection probability, prob(M|S), becomes 0.961 so his chance of a correct diagnosis in this case would be 96%.
), the probability of spots from some other cause, declines from 0.15 to 0.1. How does this change improve his rate of measles detection? What is the new prob(M|S)? With this new information, prob(S) = 0.95 × 0.2 + 0.1 × 0.8 = 0.27, so in Bayes’s formula, prob(M|S) is 0.2 divided by prob(S) = 0.27 and then all multiplied by 0.95, which comes to 0.704. So Dr Why can now detect 70% of cases with this improved information. If the probabilities changed to 0.99, and 0.01 respectively then the detection probability, prob(M|S), becomes 0.961 so his chance of a correct diagnosis in this case would be 96%.
Modern day Bayesians
The traditional statistician would have little quarrel with the use of Bayes’s formula where the probability can be measured. The contentious sticking point is interpreting probability as degrees of belief or, as it is sometimes defined subjective probability.
In a court of law, questions of guilt or innocence are sometimes decided by the ‘balance of probabilities’. Strictly speaking this criterion only applies to civil cases but we shall imagine a scenario where it applies to criminal cases as well. The frequentist statistician has a problem ascribing any meaning to the probability of a prisoner being guilty of a crime. Not so the Bayesian who does not mind taking feelings on board. How does this work? If we are to use the balance-of-probabilities method of judging guilt and innocence we now see how the probabilities can be juggled. Here is a possible scenario.
A juror has just heard a case in court and decided that the probability of the accused being guilty is about 1 in 100. During deliberations in the jury room the jury is called back into court to hear further evidence from the prosecution. A weapon has been found in the prisoner’s house and the leading prosecution counsel claims that the probability of finding it is as high as 0.95 if the prisoner is guilty, but if he is innocent the probability of finding the weapon would be only 0.1. The probability of finding a weapon in the prisoner’s house is therefore much higher if the prisoner is guilty than if they are innocent. The question before the juror is how should they modify their opinion of the prisoner in the light of this new information? Using our notation again, G is the event that the prisoner is guilty and E is the event that new evidence is obtained. The juror has made an initial assessment that prob(G) = 1/100 or 0.01. This probability is called the prior probability. The reassessment probability prob(G | E) is the revised probability of guilt given the new evidence E, and this is called the posterior probability. Bayes’s formula in the form
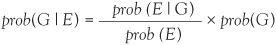
shows the idea of the prior probability being updated to the posterior probability prob(G | E). Like working out prob(S) in the medical example, we can work out prob(E) and we find
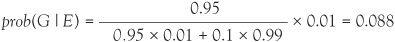
This will present a quandary for the juror because the initial assessment of a 1% chance of guilt has risen to almost 9%. If the prosecution had made the greater claim that the probability of finding the incriminating weapon was as high as 0.99 if the prisoner is guilty but if innocent the probability of finding the weapon was only 0.01, then repeating the Bayes’s formula calculation the juror would have to revise their opinion from 1% to 50%.
Using Bayes’s formula in such situations has been exposed to criticisms. The leading thrust has been on how one arrives at the prior probability. In its favour Bayesian analysis presents a way of dealing with subjective probabilities and how they may be updated based on evidence. The Bayesian method has applications in areas as diverse as science, weather forecasting and criminal justice. Its proponents argue its soundness and pragmatic character in dealing with uncertainty. It has a lot going for it.
the condensed idea
Updating beliefs using evidence

 الاكثر قراءة في هل تعلم
الاكثر قراءة في هل تعلم
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















