e is the new kid on the block when compared with its only rival π . While π is more august and has a grand past dating back to the Babylonians, e is not so weighed down by the barnacles of history. The constant e is youthful and vibrant and is ever present when ‘growth’ is involved. Whether it’s populations, money or other physical quantities, growth invariably involves e.
e is the number whose approximate value is 2.71828. So why is that so special? It isn’t a number picked out at random, but is one of the great mathematical constants. It came to light in the early 17th century when several mathematicians put their energies into clarifying the idea of a logarithm, the brilliant invention that allowed the multiplication of large numbers to be converted into addition.
But the story really begins with some 17th-century e-commerce. Jacob Bernoulli was one of the illustrious Bernoullis of Switzerland, a family which made it their business to supply a dynasty of mathematicians to the world. Jacob set to work in 1683 with the problem of compound interest.
Money, money, money
Suppose we consider a 1-year time period, an interest rate of a whopping 100%, and an initial deposit (called a ‘principal’ sum) of £1. Of course we rarely get 100% on our money but this figure suits our purpose and the concept can be adapted to realistic interests rates like 6% and 7%. Likewise, if we have greater principal sums like £10,000 we can multiply everything we do by 10,000.
At the end of the year at 100% interest, we will have the principal and the amount of interest earned which in this case is also £1. So we shall have the princely sum of £2. Now we suppose that the interest rate is halved to 50% but is applied for each half-year separately. For the first half-year we gain an interest of 50 pence and our principal has grown to £1.50 by the end of the first half-year. So, by the end of the full year we would have this amount and the 75 pence interest on this sum. Our £1 has grown to £2.25 by the end of the year! By compounding the interest each half-year we have made an extra 25 pence. It may not seem much but if we had £10,000 to invest, we would have £2,250 interest instead of £2,000. By compounding every half-year we gain an extra £250.
But if compounding every half-year means we gain on our savings, the bank will also gain on any money we owe – so we must be careful! Suppose now that the year is split into four quarters and 25% is applied to each quarter. Carrying out a similar calculation, we find that our £1 has grown to £2.44141. Our money is growing and with our £10,000 it would seem to be advantageous if we could split up the year and apply the smaller percentage interest rates to the smaller time intervals.
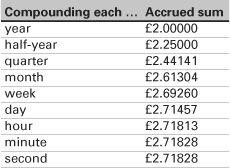
Will our money increase beyond all bounds and make us a millionaires? If we keep dividing the year up into smaller and smaller units, as shown in the table, this ‘limiting process’ shows that the amount appears to be settling down to a constant number. Of course, the only realistic compounding period is per day (and this is what banks do). The mathematical message is that this limit, which mathematicians call e, is the amount £1 grows to if compounding takes place continuously. Is this a good thing or a bad thing? You know the answer: if you are saving, ‘yes’; if you owe money, ‘no’. It’s a matter of ‘e-learning’.
The exact value of e
Like π, e is an irrational number so, as with π, we cannot know its exact value. To 20 decimal places, the value of e is 2.71828182845904523536…
Using only fractions, the best approximation to the value of e is 87/32 if the top and bottom of the fraction are limited to two-digit numbers. Curiously, if the top and bottom are limited to three-digit numbers the best fraction is 878/323. This second fraction is a sort of palindromic extension of the first one – mathematics has a habit of offering these little surprises. A well-known series expansion for e is given by
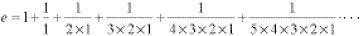
The factorial notation using an exclamation mark is handy here. In this, for example, 5! = 5×4×3×2×1. Using this notation, e takes the more familiar form
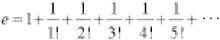
So the number e certainly seems to have some pattern. In its mathematical properties, e appears more ‘symmetric’ than π.
If you want a way of remembering the first few places of e, try this: ‘We attempt a mnemonic to remember a strategy to memorize this count…’, where the letter count of each word gives the next number of e. If you know your American history then you might remember that e is ‘2.7 Andrew Jackson Andrew Jackson’, because Andrew Jackson (‘Old Hickory’), the seventh president of the United States was elected in 1828. There are many such devices for remembering e but their interest lies in their quaintness rather than any mathematical advantage.
That e is irrational (not a fraction) was proved by Leonhard Euler in 1737. In 1840, French mathematician Joseph Liouville showed that e was not the solution of any quadratic equation and in 1873, in a path-breaking work, his countryman Charles Hermite, proved that e is transcendental (it cannot be the solution of any algebraic equation). What was important here was the method Hermite used. Nine years later, Ferdinand von Lindemann adapted Hermites’s method to prove that π was transcendental, a problem with a much higher profile.
One question was answered but new ones appeared. Is e raised to the power of e transcendental? It is such a bizarre expression, how could this be otherwise? Yet this has not been proved rigorously and, by the strict standards of mathematics, it must still be classified as a conjecture. Mathematicians have inched towards a proof, and have proved it is impossible for both it and e raised to the power of e2 to be transcendental. Close, but not close enough.
The connections between π and e are fascinating. The values of eπ and πe are close but it is easily shown (without actually calculating their values) that eπ > πe. If you ‘cheat’ and have a look on your calculator, you will see that approximate values are eπ = 23.14069 and πe = 22.45916.
The number eπ is known as Gelfond’s constant (named after the Russian mathematician Aleksandr Gelfond) and has been shown to be a transcendental. Much less is known about πe; it has not yet been proved to be irrational – if indeed it is.
Is e important?
The chief place where e is found is in growth. Examples are economic growth and the growth of populations. Connected with this are the curves depending on e used to model radioactive decay.
The number e also occurs in problems not connected with growth. Pierre Montmort investigated a probability problem in the 18th century and it has since been studied extensively. In the simple version a group of people go to lunch and afterwards pick up their hats at random. What is the probability that no one gets their own hat?
It can be shown that this probability is 1/e (about 37%) so that the probability of at least one person getting their own hat is 1 – 1/e (63%). This application in probability theory is one of many. The Poisson distribution which deals with rare events is another. These were early instances but by no means isolated ones: James Stirling achieved a remarkable approximation to the factorial value n! involving e (and π); in statistics the familiar ‘bell curve’ of the normal distribution involves e; and in engineering the curve of a suspension bridge cable depends on e. The list is endless.

An earth-shattering identity
The prize for the most remarkable formula of all mathematics involves e. When we think of the famous numbers of mathematics we think of 0, 1, π, e and the imaginary number i = √–1. How could it be that
eiπ + 1 = 0
It is! This is a result attributed to Euler.
Perhaps e’s real importance lies in the mystery by which it has captivated generations of mathematicians. All in all, e is unavoidable. Just why an author like E.V. Wright should put himself through the effort of writing an e-less novel – presumably he had a pen name too – but his Gadsby is just that. It is hard to imagine a mathematician setting out to write an e-less textbook, or being able to do so.
the condensed idea
The most natural of numbers
 الاكثر قراءة في هل تعلم
الاكثر قراءة في هل تعلم
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


